 por Ucthia » Ter Nov 18, 2008 16:29
por Ucthia » Ter Nov 18, 2008 16:29
já tentei fazer varias vezes e este exercicio não conseguiMostre que as duplas de matrizes são inversas:
a)
7 .... 4
5 .... 3
e
3 ..... - 4
-5 .... 7
ficarei mto agradecida se alguem puder responder! 
-
Ucthia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Nov 18, 2008 11:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por admin » Ter Nov 18, 2008 17:57
por admin » Ter Nov 18, 2008 17:57
Olá
Ucthia, boas-vindas!
Ucthia escreveu:já tentei fazer varias vezes e este exercicio não consegui
Tentou como?
Você poderá mostrar que as matrizes são inversas ao efetuar o produto de uma por outra e constatar uma matriz identidade como resultado, pois, sendo

uma matriz quadrada e

sua inversa, pela definição:
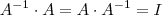
Onde

é a matriz identidade.
Neste caso, como a ordem é 2, a matriz identidade será
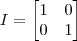
Faça o produto:
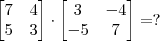
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- AJUDA COM MATRIZES
por feeh1208 » Qui Dez 08, 2011 13:10
- 1 Respostas
- 1834 Exibições
- Última mensagem por TheoFerraz

Qui Dez 08, 2011 14:52
Matrizes e Determinantes
-
- [Matrizes] ajuda !
por e8group » Seg Jun 25, 2012 17:19
- 3 Respostas
- 2127 Exibições
- Última mensagem por e8group

Ter Jun 26, 2012 00:37
Matrizes e Determinantes
-
- Ajuda com matrizes?
por Himeko » Ter Dez 02, 2014 18:53
- 1 Respostas
- 5358 Exibições
- Última mensagem por nakagumahissao

Ter Dez 02, 2014 20:11
Matrizes e Determinantes
-
- preciso de ajuda para resolver um exercicio sobre matrizes
por anabela » Sáb Nov 14, 2009 09:09
- 7 Respostas
- 7298 Exibições
- Última mensagem por Nelito

Seg Nov 16, 2009 16:56
Matrizes e Determinantes
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5165 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 uma matriz quadrada e
uma matriz quadrada e  sua inversa, pela definição:
sua inversa, pela definição: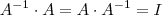
 é a matriz identidade.
é a matriz identidade.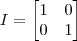
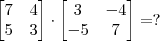

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.