Higoshi escreveu:Eu precisava de ajuda nessa questão da Santa Casa:
Simplificando a expressão (x² + 2x)².(x² - 1) / (x - 2).(x³ - x²), obtemos:
A resposta é : x² - x - 2
Bom, eu tentei abrir as duas partes mas o sinal da parte de cima não bate com a de baixo. Se alguém puder ajudar, eu agradeço.
Você quis dizer que a expressão é
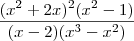
?
Se você quis dizer isso, note que o que você escreveu de fato foi
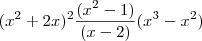
. Para escrever aquilo, você deveria ter usado algo como [(x² + 2x)².(x² - 1)]/[(x - 2).(x³ - x²)]. Tome cuidado com a precedência das operações e com o uso dos delimitadores adequados.
No caso da primeira expressão, temos que:
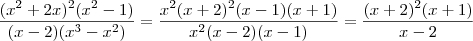
, sendo que a simplificação apenas pode ser feita se x for não nulo e diferente de 1.
Note que o gabarito indicado poderia ser esse caso tivéssemos no denominador (x-2)², como você mesmo já havia percebido.


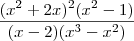 ?
?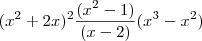 . Para escrever aquilo, você deveria ter usado algo como [(x² + 2x)².(x² - 1)]/[(x - 2).(x³ - x²)]. Tome cuidado com a precedência das operações e com o uso dos delimitadores adequados.
. Para escrever aquilo, você deveria ter usado algo como [(x² + 2x)².(x² - 1)]/[(x - 2).(x³ - x²)]. Tome cuidado com a precedência das operações e com o uso dos delimitadores adequados.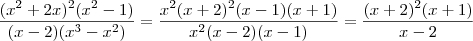 , sendo que a simplificação apenas pode ser feita se x for não nulo e diferente de 1.
, sendo que a simplificação apenas pode ser feita se x for não nulo e diferente de 1.


 , avisa que eu resolvo.
, avisa que eu resolvo.

