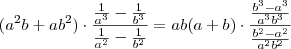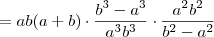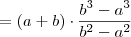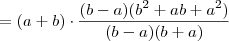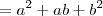-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480217 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539512 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503409 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 727460 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2163843 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por runksoneck » Dom Mar 13, 2011 16:42
por runksoneck » Dom Mar 13, 2011 16:42
Se a e b são números reais não nulos, então, simplificando a expressão, obtém-se :
(a²b+ab²). 1/a³-1/b³
........... -------------
........... 1/a²-1/b³
a²+ab+b²
Tentei, tentei e não cheguei nesse resultado.
-
runksoneck
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Fev 19, 2011 18:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Dom Mar 13, 2011 21:52
por Molina » Dom Mar 13, 2011 21:52
runksoneck escreveu:Se a e b são números reais não nulos, então, simplificando a expressão, obtém-se :
(a²b+ab²). 1/a³-1/b³
........... -------------
........... 1/a²-1/b³
a²+ab+b²
Tentei, tentei e não cheguei nesse resultado.
Boa noite, amigo.
Procure utilizar o
Editor de Fórmulas para criar expressões matemáticas deste tipo. Perceba que não é possível ter
certeza da sua expressão.
Seria isso?
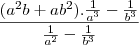
Fico no aguardo de sua confirmação.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por runksoneck » Qui Mar 17, 2011 11:34
por runksoneck » Qui Mar 17, 2011 11:34
Nesse exato momento eu não estou com tempo para aprender a mexer nesse editor. Então, só pra esclarecer:
1/a³-1/b³ / 1/a²-1/b³ e não sobre todo numerador.
Obrigado pela atenção.

-
runksoneck
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Fev 19, 2011 18:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Mar 17, 2011 12:19
por LuizAquino » Qui Mar 17, 2011 12:19
runksoneck escreveu:Nesse exato momento eu não estou com tempo para aprender a mexer nesse editor. Então, só pra esclarecer:
1/a³-1/b³ / 1/a²-1/b³ e não sobre todo numerador.
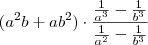
Código LaTeX usado para escrever essa expressão:
- Código: Selecionar todos
[tex](a^2b+ab^2) \cdot \frac{\frac{1}{a^3}-\frac{1}{b^3}}{\frac{1}{a^2}-\frac{1}{b^3}}[/tex]
Se você pretende tirar suas dúvidas aqui no Fórum, recomendo fortemente que arranje tempo para aprender a usar as ferramentas que ele possui.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por runksoneck » Qui Mar 17, 2011 12:29
por runksoneck » Qui Mar 17, 2011 12:29
LuizAquino escreveu:
Se você pretende tirar suas dúvidas aqui no Fórum, recomendo fortemente que arranje tempo para aprender a usar as ferramentas que ele possui.
OK, seguirei sua recomendação.
Enfim, alguém pode me ajudar dessa vez ?
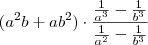
-
runksoneck
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Fev 19, 2011 18:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 6759 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- (EPCAR)conjuntos
por natanskt » Sex Out 15, 2010 18:18
- 3 Respostas
- 1740 Exibições
- Última mensagem por DanielRJ

Sex Out 15, 2010 23:07
Funções
-
- (EPCAR)função
por natanskt » Sex Out 15, 2010 23:59
- 1 Respostas
- 1094 Exibições
- Última mensagem por Elcioschin

Sáb Out 16, 2010 18:56
Funções
-
- (EPCAR)função
por natanskt » Ter Out 19, 2010 10:31
- 1 Respostas
- 1910 Exibições
- Última mensagem por MarceloFantini

Ter Out 19, 2010 17:49
Funções
-
- (EPCAR) MATRIZ
por natanskt » Qua Nov 17, 2010 16:34
- 0 Respostas
- 827 Exibições
- Última mensagem por natanskt

Qua Nov 17, 2010 16:34
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


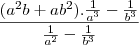


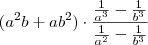
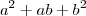 , a expressão deveria ser
, a expressão deveria ser 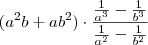 .
.