gostaria de ajuda nessa questão:
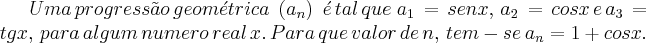
As alternativas são:
a) 4 b) 5 c) 6 d) 7 e) 8
Tentei resolvê-la através da propriedade da PG que diz que um termo médio de dois equidistantes deste é a média geométrica dos dois números.
Entretanto, não consegui resolver.
Obrigada,
Jéssica.


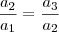 , com
, com 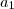 e
e 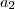 não nulos. Disso, nós obtemos que:
não nulos. Disso, nós obtemos que: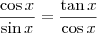
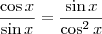
 (vamos identificar essa equação como (a))
(vamos identificar essa equação como (a))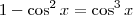
 :
: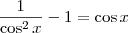
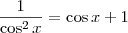 (vamos identificar essa equação como (b))
(vamos identificar essa equação como (b))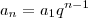 , onde
, onde 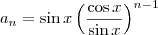 .
.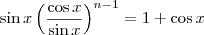 .
.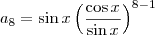
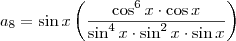
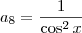

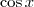 ):
):![(\cos x)^{\frac{3}{2}} \left[\frac{\cos x}{(\cos x)^{\frac{3}{2}}}\right]^{n-1} = (\cos x)^{-2} (\cos x)^{\frac{3}{2}} \left[\frac{\cos x}{(\cos x)^{\frac{3}{2}}}\right]^{n-1} = (\cos x)^{-2}](/latexrender/pictures/08df63b8b622d55869938e6d324d1671.png)
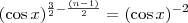
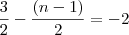
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.