Uma dúvida de combinatória

[lucasla]

Estou com uma dúvida em uma questão simples de Arranjos, até já resolvi a questão, mas uma dúvida ficou:

A questão é a seguinte: Tenho um conjunto de 9 números {1, 2, 3, 4, 5, 6, 7, 8, 9}, e quero saber quantos grupos de 7 elementos distintos posso formar com esses números, de modo que os números 5 e 6 fiquem sempre juntos e nessa mesma ordem.

Eu resolvi a questão da seguinte maneira:

Imaginando 7 espaços, os 2 primeiros espaços são reservados para o 5 e o 6, e os outros espaços vão ser arranjos de 7 elementos 5 a 5. E como o 5 e o 6 podem mudar de posição 6 vezes, multiplico esse arranjo por 6. Ou seja A7,5 * 6 = 15120 elementos diferentes. (que é a resposta correta)
_1_ x _1_ x _7_ x _6 x _5_ x _4_ x _3_ (*6) = 15120

blz, mas fazendo da seguinte maneira, que eu imaginava que também devia dar certo, não obtenho o mesmo resultado:

Como o 5 e o 6 ficarão sempre juntos e nessa ordem, posso imaginá-los como sendo um único elemento que gasta apenas 1 espaço (posso mesmo?), logo teria 8 elementos {1, 2, 3, 4, 5-6, 7, 8, 9} e 6 espaços, bastando fazer o arranjo de 8 elementos 6 a 6. Mas isso me retorna 20160.
Por que fazer isso está errado?

[MarceloFantini]

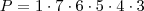Se os números 5 e 6 devem estar juntos, podemos considerá-los como um único bloco. E como também não trocam de ordem, só existe uma única maneira de posicioná-los. Logo, sobre 7 elementos distintos. Assim, o número de possibilidades será . Porém, não necessariamente os números 5 e 6 devem estar posicionados no começo. Podem ser colocados no meio, ou no final, ou depois. Enfim, a lógica é que ele pode trocar de ordem, e para representar essa troca de ordem multiplicamos por 6, que é o número de posições que ele pode ocupar: .

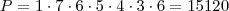[lucasla]

certo, foi assim que resolvi, mas por que que daquela segunda forma que eu tentei não funciona também?

[MarceloFantini]

Eu não me lembro a forma de arranjo, mas você tem 7 espaços para preencher e 2 já estão ocupados, portanto acredito que você também tenha que descontar essa quantidade.