porém estou tendo muita dificuldade na questão abaixo...na verdade não sei ao certo o procedimento que tenho que usar...se apenas derivar ou se seria uma integral. Gostaria mt que alguem se abilitasse a me ajudar pois estou meio desperado uma vez que minha prova vai ser aplicada amanhã e tenho muita certeza que cairá uma questão como essa!
*Uma particula que se move ao longo de uma reta tem velocidade igual a
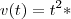 e?^-t metros por segundo após t segundos. QUal a distancia que essa particula percorre durante os t primeiro segundos?*
e?^-t metros por segundo após t segundos. QUal a distancia que essa particula percorre durante os t primeiro segundos?* Podem me responder por e-mail tambem...agradeço desde já a todos que puderem contribuir. Gabrielcoutinho13@hotmail.com



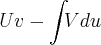 ...porém me parece muito obvio apenas integrar a fórmula
...porém me parece muito obvio apenas integrar a fórmula 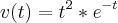 ...Qual a distancia que essa particula percorre durante os t primeiros segundos?!?!...nao teria que atribuir os numeros correspondentes? ou utilizando o TFC integrar de A ate B...com base nisso quais seriam esses valores?! Obrigadooo
...Qual a distancia que essa particula percorre durante os t primeiros segundos?!?!...nao teria que atribuir os numeros correspondentes? ou utilizando o TFC integrar de A ate B...com base nisso quais seriam esses valores?! Obrigadooo e tente integrar de 0 até t. A idéia do exercício é conseguir uma expressão para o espaço em função do tempo.
e tente integrar de 0 até t. A idéia do exercício é conseguir uma expressão para o espaço em função do tempo.

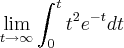 ????
???? ....obrigadooo pelas colaborações!
....obrigadooo pelas colaborações! pois é um caso particular, e fazer a integral variar de
pois é um caso particular, e fazer a integral variar de 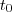 até
até  , tornando-a mais geral.
, tornando-a mais geral. .......ta osso...TA pedindo a distancia que essa particula percorre durante os t primeiros segundos!!!! E a minha resposta será uma
.......ta osso...TA pedindo a distancia que essa particula percorre durante os t primeiros segundos!!!! E a minha resposta será uma  após a integração por partes! e é isso?!?!?!
após a integração por partes! e é isso?!?!?! 
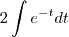 ??
??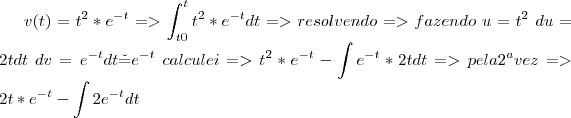
 e não como antes
e não como antes 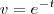 (lembre-se da regra da cadeia...)
(lembre-se da regra da cadeia...)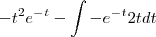 agora vc tem q resolver a segunda integral novamente por partes...
agora vc tem q resolver a segunda integral novamente por partes...![-2\int e^-^tdt = -t e^-^t - (\int -e^-^t dt) \Rightarrow 2\int e^-^tdt = 2[ t e^-^t - (\int e^-^t dt)]= -2\int e^-^tdt = -t e^-^t - (\int -e^-^t dt) \Rightarrow 2\int e^-^tdt = 2[ t e^-^t - (\int e^-^t dt)]=](/latexrender/pictures/09650da1bbdbb88965c332fb37659d5d.png)
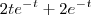
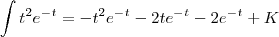 onde K é uma constante arbitraria que é uma constante arbitraria.
onde K é uma constante arbitraria que é uma constante arbitraria.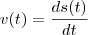 por isso, como a velocidade é uma derivada do
por isso, como a velocidade é uma derivada do 
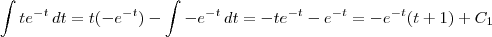
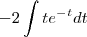 que eh a
que eh a 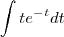 multiplicada por menos dois
multiplicada por menos dois