 por _Liilo » Ter Nov 02, 2010 16:11
por _Liilo » Ter Nov 02, 2010 16:11
![{log}_{\frac{1}{2}} \frac{\sqrt[]{2}}{2} = \frac{1}{2} {log}_{\frac{1}{2}} \frac{\sqrt[]{2}}{2} = \frac{1}{2}](/latexrender/pictures/551333c32a1d349b21a7dba84f96662c.png)
Boa tarde, no livro que utilizo há duas questão com esse cálculo e não consigo entender.
>> Qual é a base de um sistema logaritmico, onde o lagaritmo é

e o antilogaritmo é
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)
?
Sei que a base sera meio porque nos próximos exercícios aparece o seguinte:
>> Calcule o valor de "x", e modo que se tenha
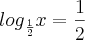
Ambos exercícios eu sei o gabarito, mas não sei como chegar na resposta fazendo o exercício.
De qualquer modo, grata.
-
_Liilo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 31, 2010 18:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: técnico em webdesign
- Andamento: formado
 por girl » Ter Nov 02, 2010 17:14
por girl » Ter Nov 02, 2010 17:14
-
girl
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 24, 2010 10:55
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por _Liilo » Ter Nov 02, 2010 18:21
por _Liilo » Ter Nov 02, 2010 18:21
oi girl,
não compreendo por que a raiz fica só no demoninador (
![\frac{1}{\sqrt[2]{2}} = x \frac{1}{\sqrt[2]{2}} = x](/latexrender/pictures/7d44153851b838dc4a225d2a5fe1e32f.png)
)
depois disso acho que vc racionaliza...
Continuo sem entender. Por favor, podes detalhar mais, explicar o porquê da
raiz de 2 ter ido como denominador.
Obrigada.
-
_Liilo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 31, 2010 18:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: técnico em webdesign
- Andamento: formado
 por girl » Ter Nov 02, 2010 19:02
por girl » Ter Nov 02, 2010 19:02
a raiz fica so no denominador por que a raiz quadrda de 1 é 1 e depois eu fiz a racionalização nos denominadores .
-
girl
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 24, 2010 10:55
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por girl » Ter Nov 02, 2010 19:13
por girl » Ter Nov 02, 2010 19:13
uma regra da potenciação é que quando vc tem um numero elevado a um expoente expresso por uma fração voce o transforma em radical.
por exemplo


o numerador da fração se torna o expoente do numero 2 e o denominador se torna o indice da raiz
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
um outro exemplo:
![{8}^{\frac{2}{3}}= \sqrt[3]{{8}^{2}}= \sqrt[3]{64} {8}^{\frac{2}{3}}= \sqrt[3]{{8}^{2}}= \sqrt[3]{64}](/latexrender/pictures/00eac0ae2a79cedfd9add79bb272a3f3.png)
-
girl
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 24, 2010 10:55
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por _Liilo » Ter Nov 02, 2010 19:39
por _Liilo » Ter Nov 02, 2010 19:39
Agora entendi \o/
Muito obrigada, girl
-
_Liilo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 31, 2010 18:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: técnico em webdesign
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derive a função: com essa mistura de raiz e frações
por SILMARAKNETSCH » Qua Nov 14, 2012 18:08
- 3 Respostas
- 2561 Exibições
- Última mensagem por SILMARAKNETSCH

Qui Nov 15, 2012 08:07
Funções
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2576 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7462 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4145 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13793 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{log}_{\frac{1}{2}} \frac{\sqrt[]{2}}{2} = \frac{1}{2} {log}_{\frac{1}{2}} \frac{\sqrt[]{2}}{2} = \frac{1}{2}](/latexrender/pictures/551333c32a1d349b21a7dba84f96662c.png)
 e o antilogaritmo é
e o antilogaritmo é ![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png) ?
?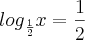


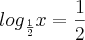 voce tem elevar a
voce tem elevar a 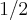 a
a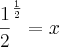
![\sqrt[2]{\frac{1}{2}}=x \sqrt[2]{\frac{1}{2}}=x](/latexrender/pictures/09d9edb0078ca741a0b74a6d8592af4f.png)
![\frac{1}{\sqrt[2]{2}}=x \frac{1}{\sqrt[2]{2}}=x](/latexrender/pictures/befd28698d2ec6910e488563017891fc.png)
![\frac{1.\sqrt[2]{2}}{{\sqrt[2]{2}}_{\sqrt[2]{2}}} \frac{1.\sqrt[2]{2}}{{\sqrt[2]{2}}_{\sqrt[2]{2}}}](/latexrender/pictures/599cca0c8a8c41338bf5afc05c4fce97.png)
![\frac{\sqrt[2]{2}}{\sqrt[2]{4}}=x \frac{\sqrt[2]{2}}{\sqrt[2]{4}}=x](/latexrender/pictures/9ba06359908689394634dd77a2d206c4.png)
![\frac{\sqrt[2]{2}}{2}=x \frac{\sqrt[2]{2}}{2}=x](/latexrender/pictures/ab64d95a887d88d0ac35189c957fd632.png)

![\frac{1}{\sqrt[2]{2}} = x \frac{1}{\sqrt[2]{2}} = x](/latexrender/pictures/7d44153851b838dc4a225d2a5fe1e32f.png) )
)
 o numerador da fração se torna o expoente do numero 2 e o denominador se torna o indice da raiz
o numerador da fração se torna o expoente do numero 2 e o denominador se torna o indice da raiz![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
![{8}^{\frac{2}{3}}= \sqrt[3]{{8}^{2}}= \sqrt[3]{64} {8}^{\frac{2}{3}}= \sqrt[3]{{8}^{2}}= \sqrt[3]{64}](/latexrender/pictures/00eac0ae2a79cedfd9add79bb272a3f3.png)


 , avisa que eu resolvo.
, avisa que eu resolvo.

