 por dsilvavinicius » Dom Jul 18, 2010 15:55
por dsilvavinicius » Dom Jul 18, 2010 15:55
Olá!
Meu problema é simples. Estou lendo um artigo e achei a seguinte notação
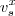
, sendo que
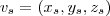
. Não consegui entendê-la. Alguém pode me ajudar?
Se alguém quiser verificar o contexto que a afirmação insere-se, o artigo é Least-squares Meshes:
http://cs.nyu.edu/~sorkine/ProjectPages ... lsmesh.pdf. Está na seção 2, página 3.
Obrigado!
-
dsilvavinicius
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jul 18, 2010 15:19
- Formação Escolar: PÓS-GRADUAÇÃO
- Andamento: cursando
 por dsilvavinicius » Dom Jul 18, 2010 15:59
por dsilvavinicius » Dom Jul 18, 2010 15:59
Favor desconsiderar, já consegui uma apresentação na qual os autores modificam a notação.
Obrigado!
-
dsilvavinicius
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jul 18, 2010 15:19
- Formação Escolar: PÓS-GRADUAÇÃO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida notação M(x,y)dy em EDO's
por dileivas » Qui Mar 15, 2012 00:22
- 2 Respostas
- 1577 Exibições
- Última mensagem por dileivas

Qui Mar 15, 2012 01:49
Cálculo: Limites, Derivadas e Integrais
-
- Notação de leibniz {dúvida}
por Danilo » Sáb Abr 27, 2013 13:15
- 2 Respostas
- 2564 Exibições
- Última mensagem por Danilo

Sáb Abr 27, 2013 15:54
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em notação científica .-.
por ThoseIAm » Ter Mar 17, 2015 21:42
- 0 Respostas
- 5164 Exibições
- Última mensagem por ThoseIAm

Ter Mar 17, 2015 21:42
Álgebra Elementar
-
- Duvida em relação a contagem de notação cientifica
por AnneEliseSalg » Qua Abr 08, 2015 20:31
- 0 Respostas
- 1331 Exibições
- Última mensagem por AnneEliseSalg

Qua Abr 08, 2015 20:31
Aritmética
-
- [ED] Notação
por Jhenrique » Sex Mai 10, 2013 17:25
- 0 Respostas
- 1467 Exibições
- Última mensagem por Jhenrique

Sex Mai 10, 2013 17:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
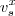 , sendo que
, sendo que 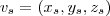 . Não consegui entendê-la. Alguém pode me ajudar?
. Não consegui entendê-la. Alguém pode me ajudar?
