 por RAISSACRIS » Qui Jul 01, 2010 23:27
por RAISSACRIS » Qui Jul 01, 2010 23:27
SOS..
CARAMBA EU TENHO QUE ENTREGAR UMAS QUESTÕES SEGUNDA FEIRA E EU NÃO CONSEQUI FAZER ALGUMAS ..E OUTRAS EU ATÉ QUE CONSEGUI.
ME AJUDEM A FAZER O QUE FALTA E VEJAM SE AS QUE EU FIZ ESTÃO OK.
1ª EQUAÇÃO DA TANGENETE ?
>>Y= TG({-X}^{2}+1), X=1>>Y=COS(frac{X}{2}) , X = 1ESSA EU REPONDI ASSIM:
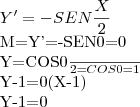
2ª UM CARTAZ DEVE CONTER 50CM² DE MATERIA IMPRESSSA COM DUAS MARGENS DE 4 CM CADA, NA PARTE SUPERIOR E NA PARTE INFERIOR E DUAS MARGENS LATERAISDE 2 CM CADA. DETERMINE AS DIMENSOÊS?
3ª DETERMINE O MAIOR COMPRIMENTO QUE DEVE TER UMA ESCADA PARA PASSAR DE UM CORREDOR DE 5 METROS DE LARGURA A OUTRO, PERPENDICULAR, DE 8 METROS DE LARGURA?
4CALCULE Y'
![Y=\sqrt[2]{2-{COS}^{2}(X)}
Y=\sqrt[2]{1-{TG}^{2}(X)}
Y={LOG}_{A}(IN(X))
Y=COT(SEC({X}^{2})
Y=\frac{SEN(2X)}{1+COS2X} Y=\sqrt[2]{2-{COS}^{2}(X)}
Y=\sqrt[2]{1-{TG}^{2}(X)}
Y={LOG}_{A}(IN(X))
Y=COT(SEC({X}^{2})
Y=\frac{SEN(2X)}{1+COS2X}](/latexrender/pictures/864d4a91a6f6c34d4b632aaf9b1c3194.png)
NÃO PRESCISA RESPONDER TODAS UMA OU DUAS OU ATE MESMO TODAS(É O QUE EU QUERO) JAH IA ME AJUDAR A NÃO REPETI A CADEIRA DE CALCULO INTEGRAL E DIFERNCIAL
ME AJUDEM PELO AMOR DE DEUS
E CASO DE VIDA OU REPEDIR O PERIODO
-
RAISSACRIS
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Jul 01, 2010 22:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: LICENCIATURA EM FISICA
- Andamento: cursando
 por DanielFerreira » Seg Jul 05, 2010 18:46
por DanielFerreira » Seg Jul 05, 2010 18:46
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Tom » Ter Jul 06, 2010 00:05
por Tom » Ter Jul 06, 2010 00:05
Não entendi o que você digitou na primeira questão, então não dá pra responder.
Vou resolver a última:
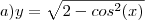
Definindo

e
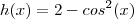
, então
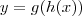
e usando a Regra da Cadeia:
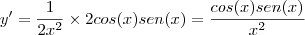
O item

é totalmente análogo ao item

, basta modificar durante a derivação da função interna.
O item

não dá pra entender o que você digiou, infelizmente.
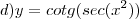
Definindo

e
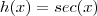
e
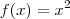
, então
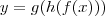
e usando a Regra da Cadeia:
![y'=g'(h(f(x))).[h(f(x))]'=g'(h(f(x))).h'(f(x)).f'(x) y'=g'(h(f(x))).[h(f(x))]'=g'(h(f(x))).h'(f(x)).f'(x)](/latexrender/pictures/a02deca9b5a12083f1113ac6e0d95a61.png)
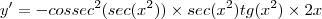
O último item, novamente, não consegui perceber o que foi digitado. Reveja os códigos, por favor.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por diogoaredes » Ter Jul 06, 2010 09:51
por diogoaredes » Ter Jul 06, 2010 09:51
Pessoal, também estou precisando de ajuda em um exercício. É o ultimo trabalho que esta faltando para mim formar na faculdade, por favor, me ajudem nisso:
1 - Um homem de 1, 80 metros de altura está parado, ao nível da rua, perto de um poste de iluminação de 4, 50 metros que está aceso. Exprima o comprimento de sua sombra como função da distância que ele está do poste.
2 - Um objeto é lançado, verticalmente, e sabe-se que no instante t segundos sua altura é dada por h(t) = 4t ? t2, em quilômetros , para 0 < t < 4.
a) Esboce o gráfico de h = h(t).
b) Qual a altura máxima atingida pelo objeto? Em que instante essa altura é atingida?
6 - Um líquido goteja em um recipiente. Após t horas, há 5t – t1/2 litros no recipiente. Qual a taxa de gotejamento de líquido no recipiente, em L/hora, quando t = 16 horas ? Justifique sua resposta
-
diogoaredes
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 06, 2010 09:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por Tom » Ter Jul 06, 2010 13:18
por Tom » Ter Jul 06, 2010 13:18
1)Imagine o homem ao lado do poste, separados por uma distância
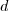
. O "raio de sol" que os ilumina feixa dois triângulos retângulos semelhantes, pois contêm ângulos iguais, de catetos:
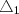
: Altura do homem , sombra do homem.
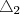
: Altura do poste, (sombra do homem+distância entre o homem e o poste).
Seja

o comprimento da sombra, da semelhança dos triângulos, temos:
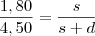
e decorre em

, isto é,
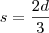
2)Eu imagino que a função horária seja:
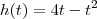
, então vou resolver com essa consideração.
a) Por análsie da função, como é regida por uma equação do segundo grau
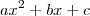
, concluímos que o gráfico é uma parábola.
Como

, concluímos que é uma parábola com concavidade voltada para baixo.
Como

, concluímos que a curva não intercepta o eixo
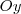
Calcule só as raízes da equação para saber as intercessoes com o eixo
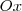
Calcule o par ordenado (
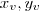
) para saber as coordenadas do ponto onde o objeto atinge a altura máxima.
Trace a curva , lembrando que o dominio é
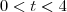
b)A altura máxima é o
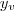
e o instante em que ela é atingida é o

.
Vamos calcular:
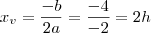
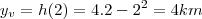
6) Vou entender que a função que mostra a quantidade de líquido no recipiente é:
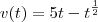
Obter a
taxa de gotejamento para
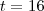
significa obter a derivada da função no ponto
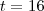
. Assim, fazemos:
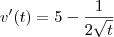
, entao
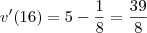
Assim, a taxa de gotejamento supracitada é
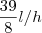
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por MarceloFantini » Ter Jul 06, 2010 18:01
por MarceloFantini » Ter Jul 06, 2010 18:01
Diogo, por favor poste a sua dúvida num novo tópico para não amontoar dúvidas num mesmo lugar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por diogoaredes » Qui Jul 08, 2010 13:03
por diogoaredes » Qui Jul 08, 2010 13:03
Pessoal, me ajudem nessas seguintes questões por favor!!!!!!
Determine a primeira derivada das seguintes funções:
![A) y = {x}^{8} + {(2x + 4)}^{3} +\sqrt[]{x}
C) y = 3x(8x{}^{3} -2)
D) y = \sqrt[3]{6x{}^{2} + 7x + 2}
E) f(x) = 10(3x{}^{2} + 7x -3){}^{10}
F) f(x)= (x{}^{5} - 4x{}^{3} - 7){}^{8} A) y = {x}^{8} + {(2x + 4)}^{3} +\sqrt[]{x}
C) y = 3x(8x{}^{3} -2)
D) y = \sqrt[3]{6x{}^{2} + 7x + 2}
E) f(x) = 10(3x{}^{2} + 7x -3){}^{10}
F) f(x)= (x{}^{5} - 4x{}^{3} - 7){}^{8}](/latexrender/pictures/1c35090de08712f5410d87d584f303ab.png)
Discuta a continuidade de cada uma das seguintes funções:
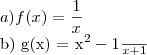
desde já agradeço a ajuda!!
-
diogoaredes
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 06, 2010 09:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por Tom » Qui Jul 08, 2010 13:04
por Tom » Qui Jul 08, 2010 13:04
Diogo, conforme ja sugerido, seria ideal você postar suas dúvidas criando outro tópico.

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por diogoaredes » Qui Jul 08, 2010 13:27
por diogoaredes » Qui Jul 08, 2010 13:27
Amigo Tom....
Até que eu tentei, mas como eu sou nome aqui não sei como criar um novo tópico... você poderia me ajudar??/
-
diogoaredes
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 06, 2010 09:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por Tom » Qui Jul 08, 2010 13:38
por Tom » Qui Jul 08, 2010 13:38
Segue a resolução:
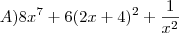
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
Nao tinha lá

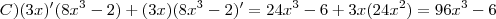
, foi usada a Regra do Produto e a Regra da função polinomial.
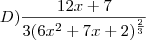
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
![E)(10)'[(3x^2+7x-3)^{10}]+10[(3x^2+7x-3)^{10}]'=10.10(3x^2+7x-3)^9(6x+7) E)(10)'[(3x^2+7x-3)^{10}]+10[(3x^2+7x-3)^{10}]'=10.10(3x^2+7x-3)^9(6x+7)](/latexrender/pictures/9813c6939a2195aaf841762513220827.png)
, foram usadas as regras : Do Produto, Da Cadeia, Das funções polinomiais.
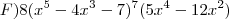
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
Discuta a continuidade de cada uma das seguintes funções:
Uma função é dita contínua em um ponto de abscissa

se:
i)
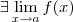
e
ii)
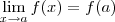
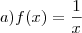
, percebemos que
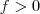
se

e
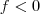
se
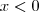
, no entanto,
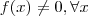
. Observa-se que os limites laterais de

para

são distintos, portanto não existe limite para
x tendendo a zero. Assim

é abicissa do ponto de descontinuidade e a função é, notavelmente, descontínua.
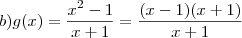
e como não estamos interessados em tornar
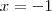
mas se em verificar o limite quando tendemos

ao valor supracitado, temos que:
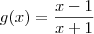
e há, notavelmente o limite para
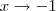
.
Ora, como toda função polinomial é contínua, o quociente supracitado é certamente contínuo. Concuímos, portanto, que

é contínua.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por MarceloFantini » Qui Jul 08, 2010 17:50
por MarceloFantini » Qui Jul 08, 2010 17:50
Diogo, quando quiser criar um novo tópico é simples: entre na área relacionada a sua dúvida, e existe um botão logo acima de onde está escrito "Sugestões e Críticas", cujo nome é Novo Tópico. Basta clicar, colocar o nome, postar a questão e pronto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por diogoaredes » Sex Jul 09, 2010 08:18
por diogoaredes » Sex Jul 09, 2010 08:18
Obrigado Fantini
-
diogoaredes
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 06, 2010 09:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12555 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10886 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13191 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14795 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5113 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
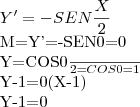
![Y=\sqrt[2]{2-{COS}^{2}(X)}
Y=\sqrt[2]{1-{TG}^{2}(X)}
Y={LOG}_{A}(IN(X))
Y=COT(SEC({X}^{2})
Y=\frac{SEN(2X)}{1+COS2X} Y=\sqrt[2]{2-{COS}^{2}(X)}
Y=\sqrt[2]{1-{TG}^{2}(X)}
Y={LOG}_{A}(IN(X))
Y=COT(SEC({X}^{2})
Y=\frac{SEN(2X)}{1+COS2X}](/latexrender/pictures/864d4a91a6f6c34d4b632aaf9b1c3194.png)


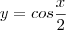
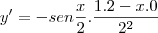
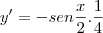
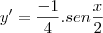
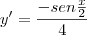
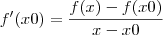
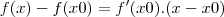
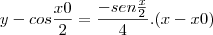
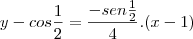

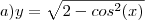
 e
e 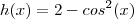 , então
, então 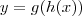 e usando a Regra da Cadeia:
e usando a Regra da Cadeia: 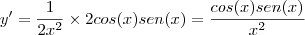
 é totalmente análogo ao item
é totalmente análogo ao item  , basta modificar durante a derivação da função interna.
, basta modificar durante a derivação da função interna. não dá pra entender o que você digiou, infelizmente.
não dá pra entender o que você digiou, infelizmente.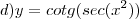
 e
e 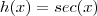 e
e 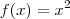 , então
, então 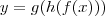 e usando a Regra da Cadeia:
e usando a Regra da Cadeia:![y'=g'(h(f(x))).[h(f(x))]'=g'(h(f(x))).h'(f(x)).f'(x) y'=g'(h(f(x))).[h(f(x))]'=g'(h(f(x))).h'(f(x)).f'(x)](/latexrender/pictures/a02deca9b5a12083f1113ac6e0d95a61.png)
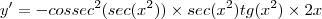

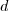 . O "raio de sol" que os ilumina feixa dois triângulos retângulos semelhantes, pois contêm ângulos iguais, de catetos:
. O "raio de sol" que os ilumina feixa dois triângulos retângulos semelhantes, pois contêm ângulos iguais, de catetos: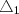 : Altura do homem , sombra do homem.
: Altura do homem , sombra do homem.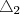 : Altura do poste, (sombra do homem+distância entre o homem e o poste).
: Altura do poste, (sombra do homem+distância entre o homem e o poste). o comprimento da sombra, da semelhança dos triângulos, temos:
o comprimento da sombra, da semelhança dos triângulos, temos: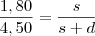 e decorre em
e decorre em  , isto é,
, isto é, 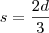
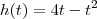 , então vou resolver com essa consideração.
, então vou resolver com essa consideração.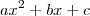 , concluímos que o gráfico é uma parábola.
, concluímos que o gráfico é uma parábola. , concluímos que é uma parábola com concavidade voltada para baixo.
, concluímos que é uma parábola com concavidade voltada para baixo. , concluímos que a curva não intercepta o eixo
, concluímos que a curva não intercepta o eixo 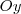
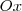
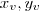 ) para saber as coordenadas do ponto onde o objeto atinge a altura máxima.
) para saber as coordenadas do ponto onde o objeto atinge a altura máxima.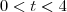
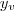 e o instante em que ela é atingida é o
e o instante em que ela é atingida é o  .
.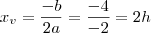
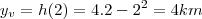
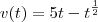
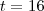 significa obter a derivada da função no ponto
significa obter a derivada da função no ponto 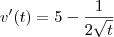 , entao
, entao 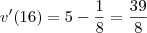
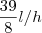


![A) y = {x}^{8} + {(2x + 4)}^{3} +\sqrt[]{x}
C) y = 3x(8x{}^{3} -2)
D) y = \sqrt[3]{6x{}^{2} + 7x + 2}
E) f(x) = 10(3x{}^{2} + 7x -3){}^{10}
F) f(x)= (x{}^{5} - 4x{}^{3} - 7){}^{8} A) y = {x}^{8} + {(2x + 4)}^{3} +\sqrt[]{x}
C) y = 3x(8x{}^{3} -2)
D) y = \sqrt[3]{6x{}^{2} + 7x + 2}
E) f(x) = 10(3x{}^{2} + 7x -3){}^{10}
F) f(x)= (x{}^{5} - 4x{}^{3} - 7){}^{8}](/latexrender/pictures/1c35090de08712f5410d87d584f303ab.png)
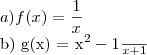
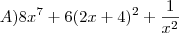 , foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
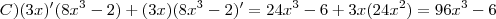 , foi usada a Regra do Produto e a Regra da função polinomial.
, foi usada a Regra do Produto e a Regra da função polinomial.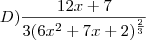 , foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.![E)(10)'[(3x^2+7x-3)^{10}]+10[(3x^2+7x-3)^{10}]'=10.10(3x^2+7x-3)^9(6x+7) E)(10)'[(3x^2+7x-3)^{10}]+10[(3x^2+7x-3)^{10}]'=10.10(3x^2+7x-3)^9(6x+7)](/latexrender/pictures/9813c6939a2195aaf841762513220827.png) , foram usadas as regras : Do Produto, Da Cadeia, Das funções polinomiais.
, foram usadas as regras : Do Produto, Da Cadeia, Das funções polinomiais.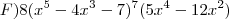 , foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.
, foi usada a Regra da Cadeia e a Regra de derivação de funções polinomiais.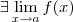 e
e 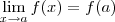
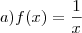 , percebemos que
, percebemos que 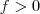 se
se  e
e 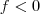 se
se 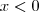 , no entanto,
, no entanto, 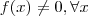 . Observa-se que os limites laterais de
. Observa-se que os limites laterais de  para
para  são distintos, portanto não existe limite para
são distintos, portanto não existe limite para  é abicissa do ponto de descontinuidade e a função é, notavelmente, descontínua.
é abicissa do ponto de descontinuidade e a função é, notavelmente, descontínua.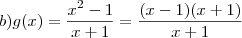 e como não estamos interessados em tornar
e como não estamos interessados em tornar 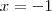 mas se em verificar o limite quando tendemos
mas se em verificar o limite quando tendemos  ao valor supracitado, temos que:
ao valor supracitado, temos que: 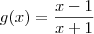 e há, notavelmente o limite para
e há, notavelmente o limite para 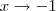 .
. é contínua.
é contínua.