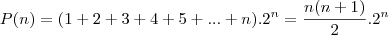O Problema:
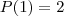
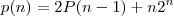
Eu fiz assim mas ta errado:
n=2 -
![2.[2P(n-2)+[n2^n-1] + n2^n 2.[2P(n-2)+[n2^n-1] + n2^n](/latexrender/pictures/460f60cbf390651c764a86d2a5f1f2ad.png)
n=3 -
![2.2.[2P(n-3)+[n2^n-2] + [n2^n -1] +n2^n 2.2.[2P(n-3)+[n2^n-2] + [n2^n -1] +n2^n](/latexrender/pictures/88f78c8fc5d0ff722055213810d8be1e.png)
n=4 -
![2.2.2.[2P(n-4)+[n2^n-3] [n2^n -2] +n2^n-1+n2^n 2.2.2.[2P(n-4)+[n2^n-3] [n2^n -2] +n2^n-1+n2^n](/latexrender/pictures/d3b1c87240d214b9db4082c4efa71627.png)
forma geral:
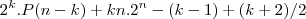
Ai fiz:
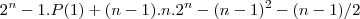
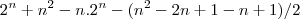
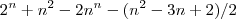
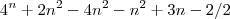
Ai deu isso aqui,mas quando substituo nao da certo.
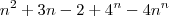
Tem uma formula tbm mas nao consegui:
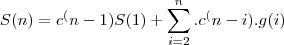
Gostaria que vcs deem dicas de como fazer la em cima so o" n2^n" , porque se fosse um numero eu saberia mas"elevado à n" ta complicado.Se vcs puderem ajudar estarei mt grato.Obrigado


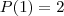
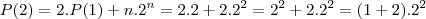
![P(3) = 2.P(2) + 3.2^3 = 2 .[(1+2).2^2] + 3.2^3 = (1+2+3).2^3 P(3) = 2.P(2) + 3.2^3 = 2 .[(1+2).2^2] + 3.2^3 = (1+2+3).2^3](/latexrender/pictures/4265f6482701e1ceddae66daa6875096.png)
![P(4) = 2.P(3) + 4.2^4 = 2.[(1+2+3).2^3] + 4.2^4 = (1+2+3+4).2^4 P(4) = 2.P(3) + 4.2^4 = 2.[(1+2+3).2^3] + 4.2^4 = (1+2+3+4).2^4](/latexrender/pictures/36a786b152bba4b9e85d8d509fd66762.png)
![P(5) = 2.P(4) + 5.2^5 = 2.[(1+2+3+4).2^4] + 5.2^5 = (1+2+3+4+5).2^5 P(5) = 2.P(4) + 5.2^5 = 2.[(1+2+3+4).2^4] + 5.2^5 = (1+2+3+4+5).2^5](/latexrender/pictures/afc34215ee3990bb1c6d1d836eb75a67.png)