 por viniseni567 » Qua Jan 01, 2020 17:16
por viniseni567 » Qua Jan 01, 2020 17:16
![x=\frac{(2+\sqrt[]{3})^1^9^9^7+(2-\sqrt[]{3})^1^9^9^7}{2} x=\frac{(2+\sqrt[]{3})^1^9^9^7+(2-\sqrt[]{3})^1^9^9^7}{2}](/latexrender/pictures/acd4904dfff73bed29ec62f3293162e6.png)
e
![y=\frac{(2+\sqrt[]{3})^1^9^9^7-(2-\sqrt[]{3})^1^9^9^7}{2} y=\frac{(2+\sqrt[]{3})^1^9^9^7-(2-\sqrt[]{3})^1^9^9^7}{2}](/latexrender/pictures/d1d5d151cca658113716605d6afa522f.png)
. Então o valor de
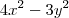
é:
Eu encontrei o valor do X, porém o Y que encontro é sempre:
![{(2+\sqrt[]{3})^3^9^9^4-2+(2-\sqrt[]{3})^3^9^9^4}{} {(2+\sqrt[]{3})^3^9^9^4-2+(2-\sqrt[]{3})^3^9^9^4}{}](/latexrender/pictures/d9d018cf4ac085d165812e980272bd7a.png)
Poderiam me explicar por que o Y dessa expressão tem o resultado de gabarito
![(2+\sqrt[]{3})^3^9^9^4+2+(2-\sqrt[]{3})^3^9^9^4 (2+\sqrt[]{3})^3^9^9^4+2+(2-\sqrt[]{3})^3^9^9^4](/latexrender/pictures/1c21ef586feedcfa22070493afe826fb.png)
; que
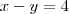
PS: Eu passei 6 horas revisando o jogo de sinais e os produtos notáveis, mas sempre chego ao resultado, com o sinal de negativo; logo chegando ao resultado 2.
-
viniseni567
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jan 01, 2020 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: enfermagem
- Andamento: cursando
 por adauto martins » Sex Jan 03, 2020 17:20
por adauto martins » Sex Jan 03, 2020 17:20
faz-se
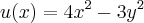
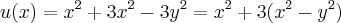
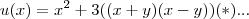
´
![x+y={(2+\sqrt[]{3})}^{1997}
x-y={(2- \sqrt[]{3})}^{1997} x+y={(2+\sqrt[]{3})}^{1997}
x-y={(2- \sqrt[]{3})}^{1997}](/latexrender/pictures/3e304e3448abed7108ee6f8625e267b4.png)
´
substitui em (*)...termine-o
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potência de raiz de raiz com subtração
 por Sergio filho » Sáb Dez 05, 2015 08:50
por Sergio filho » Sáb Dez 05, 2015 08:50
- 1 Respostas
- 1912 Exibições
- Última mensagem por Sergio filho

Dom Dez 06, 2015 11:22
Equações
-
- Expressão Álgebrica
por Daniel Gurgel » Ter Set 29, 2009 15:27
- 1 Respostas
- 2234 Exibições
- Última mensagem por DanielFerreira

Qua Set 30, 2009 09:24
Álgebra Elementar
-
- expressão algébrica
por Gustavo R » Sáb Out 08, 2011 16:33
- 1 Respostas
- 2001 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 09:03
Álgebra Elementar
-
- expressão algébrica
por 1000ton » Dom Nov 06, 2011 14:17
- 2 Respostas
- 3595 Exibições
- Última mensagem por Neperiano

Sex Nov 11, 2011 16:23
Álgebra Elementar
-
- expressão algébrica
por Andreza » Qui Jan 19, 2012 11:30
- 1 Respostas
- 1792 Exibições
- Última mensagem por Arkanus Darondra

Qui Jan 19, 2012 12:31
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x=\frac{(2+\sqrt[]{3})^1^9^9^7+(2-\sqrt[]{3})^1^9^9^7}{2} x=\frac{(2+\sqrt[]{3})^1^9^9^7+(2-\sqrt[]{3})^1^9^9^7}{2}](/latexrender/pictures/acd4904dfff73bed29ec62f3293162e6.png) e
e ![y=\frac{(2+\sqrt[]{3})^1^9^9^7-(2-\sqrt[]{3})^1^9^9^7}{2} y=\frac{(2+\sqrt[]{3})^1^9^9^7-(2-\sqrt[]{3})^1^9^9^7}{2}](/latexrender/pictures/d1d5d151cca658113716605d6afa522f.png) . Então o valor de
. Então o valor de 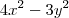 é:
é:![{(2+\sqrt[]{3})^3^9^9^4-2+(2-\sqrt[]{3})^3^9^9^4}{} {(2+\sqrt[]{3})^3^9^9^4-2+(2-\sqrt[]{3})^3^9^9^4}{}](/latexrender/pictures/d9d018cf4ac085d165812e980272bd7a.png)
![(2+\sqrt[]{3})^3^9^9^4+2+(2-\sqrt[]{3})^3^9^9^4 (2+\sqrt[]{3})^3^9^9^4+2+(2-\sqrt[]{3})^3^9^9^4](/latexrender/pictures/1c21ef586feedcfa22070493afe826fb.png) ; que
; que 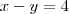


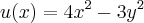
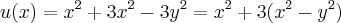
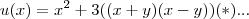 ´
´![x+y={(2+\sqrt[]{3})}^{1997}
x-y={(2- \sqrt[]{3})}^{1997} x+y={(2+\sqrt[]{3})}^{1997}
x-y={(2- \sqrt[]{3})}^{1997}](/latexrender/pictures/3e304e3448abed7108ee6f8625e267b4.png) ´
´
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.