eu tenho esse limite (já resolvido):

Ele foi resolvido dessa forma:

Eu gostaria de saber o porquê disso
 ser
ser  .
.Será que eu estou confundindo alguma coisa? Eu tentei entender e realmente não consegui. Obrigado desde já.



 ser
ser  .
.
GandalfOAzul escreveu:Eu gostaria de saber o porquê dissoser
.


GandalfOAzul escreveu:Eu gostaria de saber o porquê dissoser
.


Lembre-se do Limite fundamental
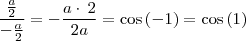



 . Assim,
. Assim,![\\ \displaystyle \mathsf{\lim_{x \to a} = \frac{\sin x - \sin a}{x - a} =} \\\\\\ \mathsf{\lim_{x - a \to 0} \frac{\sin (k + a) - \sin a}{(k + a) - a} = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin (k + a) - \sin a}{k + a - a} = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin k \cdot \cos a + \sin a \cdot \cos k - \sin a}{k} = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin k \cdot \cos a + \sin a \cdot \left ( \cos k - 1 \right )}{k} = } \\\\\\ \mathsf{\lim_{k \to 0} \left [ \frac{\sin k \cdot \cos a + \sin a \cdot \left ( \cos k - 1 \right )}{k} \right ] = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin k \cdot \cos a}{k} + \lim_{k \to 0} \frac{\sin a \cdot \left ( \cos k - 1 \right )}{k} = } \\\\\\ \mathsf{\cos a \cdot \underbrace{\mathsf{\lim_{k \to 0} \frac{\sin k}{k}}}_{limite \ fundamental} + \sin a \cdot \underbrace{\mathsf{\lim_{k \to 0} \frac{\left ( \cos k - 1 \right )}{k}}}_{zero} = } \\\\ \mathsf{\cos a \cdot 1 + \sin a \cdot 0 =} \\\\ \boxed{\mathsf{\cos a}} \\ \displaystyle \mathsf{\lim_{x \to a} = \frac{\sin x - \sin a}{x - a} =} \\\\\\ \mathsf{\lim_{x - a \to 0} \frac{\sin (k + a) - \sin a}{(k + a) - a} = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin (k + a) - \sin a}{k + a - a} = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin k \cdot \cos a + \sin a \cdot \cos k - \sin a}{k} = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin k \cdot \cos a + \sin a \cdot \left ( \cos k - 1 \right )}{k} = } \\\\\\ \mathsf{\lim_{k \to 0} \left [ \frac{\sin k \cdot \cos a + \sin a \cdot \left ( \cos k - 1 \right )}{k} \right ] = } \\\\\\ \mathsf{\lim_{k \to 0} \frac{\sin k \cdot \cos a}{k} + \lim_{k \to 0} \frac{\sin a \cdot \left ( \cos k - 1 \right )}{k} = } \\\\\\ \mathsf{\cos a \cdot \underbrace{\mathsf{\lim_{k \to 0} \frac{\sin k}{k}}}_{limite \ fundamental} + \sin a \cdot \underbrace{\mathsf{\lim_{k \to 0} \frac{\left ( \cos k - 1 \right )}{k}}}_{zero} = } \\\\ \mathsf{\cos a \cdot 1 + \sin a \cdot 0 =} \\\\ \boxed{\mathsf{\cos a}}](/latexrender/pictures/30c5e138658f7e08eef1f43c4915d409.png)

DanielFerreira escreveu:GandalfOAzul, revendo minha resposta e sua dúvida, percebo certa distância... Desculpe-me!!
Tem outro caminho... Espero que seja mais fácil de compreender, caso contrário, comente!



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)