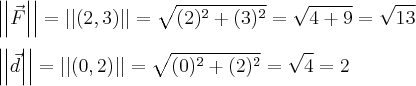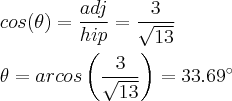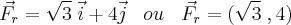Novamente, o erro na tua resolução não é quanto as contas, mas sim quanto a identificação dos catetos.
Se tu troca o oposto pelo adjacente o angulo também vai mudar.
É essencial que tu desenhe o plano cartesiano e os vetores nele para que assim tu possa identificar corretamente os catetos.
A figura que eu postei em uma das msgs anteriores exemplifica este desenho, porem vou colocar mais um em anexo.
Perceba que inclusive tu estas calculando o cateto oposto, no entanto nao é necessario, pois ja temos o seu valor que é 3.
A hipotenusa pode ser calculada por pitagoras ou basta lembrar olhando pra figura que ela tem o mesmo tamanho do vetor (modulo do vetor).
A questão 4 precisa que seja primeiro calculado o vetor força resultante.
-> Temos 3 forças, duas são verticais ( F1 e F3) e outra faz 30° com a horizontal (F2).
-> A força F2 pode ser decomposta em duas forças, uma horizontal ( F2cos(30°) ) e outra vertical ( F2sen(30°) ).
-> Somando as componentes verticais temos: F1 + F3 + F2sen(30°) = 4 + (-1) + 2sen(30°) = 3 + 1 = 4
-> Somando as componentes horizontais temos: F2cos(30°) = 2* ( Raiz(3) / 2 ) = Raiz(3)
-> Vetor Fr fica então:
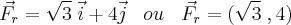
-> Pra calcular o trabalho precisamos do vetor deslocamento que, como discutido anteriormente, nao foi dado.





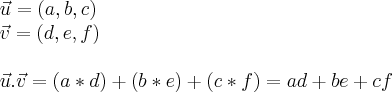
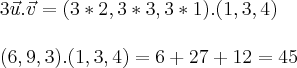
 . Perceba também que nesta equação precisamos do cosseno do angulo entre os dois vetores.
. Perceba também que nesta equação precisamos do cosseno do angulo entre os dois vetores.