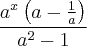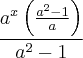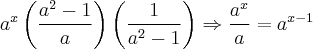por danielneiva » Sáb Ago 20, 2016 13:31
por danielneiva » Sáb Ago 20, 2016 13:31
"Se
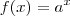
, pode-se afirquer que
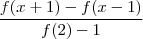
é igual a:
(A) f(x-1)
(B) f(x)
(C) f(x+1)
(D) f(-x)"
Eu vi a resolução dessa questão, e após substituir as funções ficou
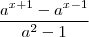
Logo após colocaram
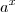
e ficou
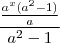
Eu não entendi como que funcionou essa evidência, porquê colocou
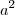
dentro do parênte...
Desde já obrigado! =D
-
danielneiva
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 16, 2016 22:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Sáb Ago 20, 2016 17:28
por Cleyson007 » Sáb Ago 20, 2016 17:28
Olá, boa tarde amigo!
Estou partindo do pressuposto que tenhas entendido a substituição (caso não tenha, me comunique por favor). Vamos lá:
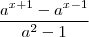

Agora sim, vamos colocar o termo
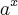
em evidência:
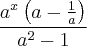
Prosseguindo...
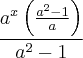
Apenas tirou-se o mmc dentro do parêntese!
Usando a regra da divisão de frações:
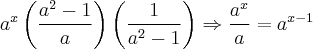
Logo, a alternativa correta é a
letra A.
--> Sou professor de Matemática e tenho um e-mail destinado a resolução de exercícios. Talvez tenha interesse em conhecer o nosso trabalho, acesse:
viewtopic.php?f=151&t=13614Atendo também pelo WhatsApp: (38) 9 9889 5755
Bons estudos
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por danielneiva » Sáb Ago 20, 2016 22:28
por danielneiva » Sáb Ago 20, 2016 22:28
Muito obrigado Cleyson!
-
danielneiva
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 16, 2016 22:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- /fATOR COMUM EM EVIDENCIA ME AJUDEM !!!!
por Reidson » Dom Ago 04, 2013 23:56
- 1 Respostas
- 1317 Exibições
- Última mensagem por Russman

Seg Ago 05, 2013 07:36
Álgebra Elementar
-
- como se acha a p.a nesse caso?
por Dalila » Sex Nov 14, 2008 16:14
- 2 Respostas
- 3062 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 16:45
Progressões
-
- Função - Como proceder nesse caso?
por micheel » Dom Ago 18, 2013 22:37
- 1 Respostas
- 1996 Exibições
- Última mensagem por Russman

Dom Ago 18, 2013 23:16
Funções
-
- Como faço?
por mtuliopaula » Qui Nov 12, 2009 18:04
- 2 Respostas
- 3371 Exibições
- Última mensagem por mtuliopaula

Sex Nov 13, 2009 15:56
Estatística
-
- Como faço?
por Liliani » Seg Mar 15, 2010 16:23
- 1 Respostas
- 1698 Exibições
- Última mensagem por Molina

Seg Mar 15, 2010 17:30
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
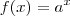 , pode-se afirquer que
, pode-se afirquer que 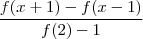 é igual a:
é igual a: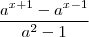
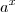 e ficou
e ficou 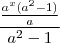
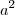 dentro do parênte...
dentro do parênte...


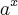 em evidência:
em evidência: