Olá, jovens, essa é minha primeira dúvida aqui, entao perdoem quaisquer erros de conduta, por favor. Vamos ao ex:
Sabendo que a altura de um triângulo relativa a hipotenusa é 12, exprima o comprimento da hipotenusa em função do perímetro de tal triângulo.
Chamemos os catetos de A e B, hipotenusa de C.
Por semelhança entre de triângulos vem: 12/A=B/C de onde B = 12C/A (I)
Substituindo B no Teorema de Pitágoras vem: 144C²/A² + A² = C² de onde acharíamos A em função de C para depois substituir em (I) e achar B em função de C.
Dessa forma, a equação do perímetro 2p = A + B + C ficaria em função de C, de onde poderíamos finalmente tirar a resposta do exercício.
O problema é aquela equação biquadrada que é gerada pelo teorema de pitágoras, cuja solução leva a uma resolução extremamente trabalhosa. Por isso estou em dúvida se minha abordagem está correta e/ou se há mais jeitos de fazer o exercício.
Desde já obrigado!
...
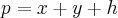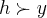(por que?)![\Rightarrow h=12y\Rightarrow x=\sqrt[]{{h}^{2}-{y}^{2}}](/latexrender/pictures/c858fdd4d35b3174f65eee55d0cc0f35.png "\Rightarrow h=12y\Rightarrow x=\sqrt[]{{h}^{2}-{y}^{2}}")
...o problema pede ![p=f(h)\Rightarrow p=\sqrt[]{{h}^{2}-{(h/12)}^{2}}+h/12+h](/latexrender/pictures/73b7d4a4e68ba584ee894fce7eb3be48.png "p=f(h)\Rightarrow p=\sqrt[]{{h}^{2}-{(h/12)}^{2}}+h/12+h")
...ai é fazer as contas e...
![p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)](/latexrender/pictures/f3ee42eb2b73b0e82a967949a486d678.png "p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)")
![p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)\Rightarrow h=12p.(\sqrt[]{143}-13)/(143-169)=12p.(13-\sqrt[]{143})/26](/latexrender/pictures/a7539ee6e5341404e0b3268d2c009655.png "p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)\Rightarrow h=12p.(\sqrt[]{143}-13)/(143-169)=12p.(13-\sqrt[]{143})/26")
![\Rightarrow h=(6/13).(13-\sqrt[]{143})p](/latexrender/pictures/1420d983723b87d9cf63dbe89758cd0a.png "\Rightarrow h=(6/13).(13-\sqrt[]{143})p")
...
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)