 por zenildo » Qui Mai 19, 2016 13:03
por zenildo » Qui Mai 19, 2016 13:03
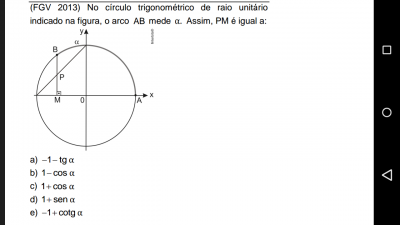
Segue anexo um problema. Este problema não consegui resolver devido eu não saber interpreta-lo.
- Anexos
-
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Daniel Bosi » Qui Mai 19, 2016 15:32
por Daniel Bosi » Qui Mai 19, 2016 15:32
Analisando a figura perceba o seguinte: a distância do ponto M até o 0 é o cosseno de

em radianos. A distância do "início" do eixo x à esquerda até o M deve ser a mesma distância de M até P (pois a reta inclinada faz um ângulo de 45 graus). Assim sendo, é razoável concluir que a distância de M até P é

, lembrando que este ciclo trigonométrico tem raio 1.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por zenildo » Qui Mai 19, 2016 18:50
por zenildo » Qui Mai 19, 2016 18:50
Resolvi fazer deste modo. Então, fiz as representações, porém não consegui finalizar os cálculos. Alguém poderia me ajudar a compreender?
- Anexos
-

-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Daniel Bosi » Qui Mai 19, 2016 23:17
por Daniel Bosi » Qui Mai 19, 2016 23:17
Zenildo, perceba que o que você representou como 0M é o
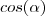
. Basta substituir.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Daniel Bosi » Sex Mai 20, 2016 09:57
por Daniel Bosi » Sex Mai 20, 2016 09:57
Zenildo, percebi um detalhe que fugiu da minha interpretação: nesse quadrante o cosseno é negativo, o que significa que o resultado de
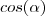
será negativo. Portanto, para a resposta ser o comprimento de M até P, é necessário mudar o sinal e o resultado fica
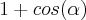
.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por zenildo » Sex Mai 20, 2016 10:25
por zenildo » Sex Mai 20, 2016 10:25
MB.MN = MQ.MA equivalente a:
Entende-se o ponto médio (M) ser equidistante entre MB e MN. Dessa forma, evidencia-se adotar: MB.MB, como MB^2.
Outro ponto importante, é perceber uma equidistancia também entre: MO=MQ. Então, se eu escrevo:
MO = (1-PM).Por outro lado, ora, se eu tenho MA, tenho, pois, o raio valendo um e operando de dois lados. Soma-se 2. Sendo 2-PM, porque MB^2 equivale a mesma distância em relação a linha horizontal, ficando MB^2= PM(2-PM).
Eis então a fórmula abaixo:
MB.MN = MQ. MA
MB^2= PM.(2-PM)
Veja se meu raciocínio esta certo ou errado,ou, se tem alguma forma de fazer que possibilite acertar com mais intuitividade.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Daniel Bosi » Sex Mai 20, 2016 11:21
por Daniel Bosi » Sex Mai 20, 2016 11:21
A meu ver é mais simples que isso. Particularmente, eu não vejo a necessidade de operar tanto com segmentos de reta. O que é importante é perceber de cara que o segmento M0 é o
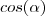
. Basta perceber que:
(1) MQ = MP (o segmento MQ e MP têm o mesmo tamanho)
(2) MQ + M0 = 1 (a soma de MQ com M0 é o raio do círculo)
De (1) sabemos que MQ = MP, basta substituir MQ em (2):
MP + M0 = 1
Agora basta perceber que M0 é o cosseno do comprimento

, pois M0 é um comprimento que parte do ponto 0 no eixo dos cossenos e corresponde ao comprimento do arco.
O porém, como eu comentei anteriormente, é que esse cosseno dá um resultado negativo entre 0 e -1. Portanto, para obter o comprimento de MP é necessário expressar a resposta como
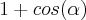
.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por zenildo » Sex Mai 20, 2016 13:55
por zenildo » Sex Mai 20, 2016 13:55
Estaria certo desse modo que interpretei? Apesar de não saber se está matematicamente correto. Poderia corrigir?
- Anexos
-
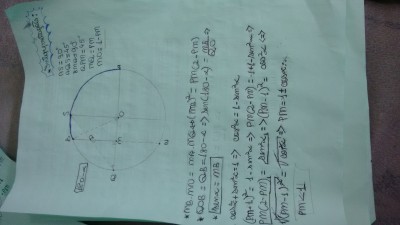
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Daniel Bosi » Sex Mai 20, 2016 14:38
por Daniel Bosi » Sex Mai 20, 2016 14:38
Zenildo, na realidade eu não entendo o que você quer dizer quando expressa MB.MN, por exemplo. Você poderia explicar para que eu possa entender essa notação?
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por zenildo » Seg Mai 23, 2016 13:13
por zenildo » Seg Mai 23, 2016 13:13
Quis fazer simplesmente uma demonstração geral. Sendo que, essa demonstração explica a sua orientação direta de como fazer o raciocínio. Nada demais.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por zenildo » Seg Mai 23, 2016 13:24
por zenildo » Seg Mai 23, 2016 13:24
Quanto a relação MB.MN, se deu por meio de serem simétricos ao ponto M.Entao,o produto dos dois, MB. MB, correspondem a igualdade.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por adauto martins » Ter Mai 24, 2016 13:20
por adauto martins » Ter Mai 24, 2016 13:20
considere o ponto C(-1,0)...logo temos q. MP=MC=x(mostre isto,é facil por semelhança de triang. ou angulo interno)...logo teremos
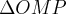
q.

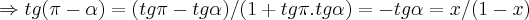
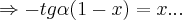
e ai é isolar o x,resolva o restante...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por zenildo » Sáb Jun 18, 2016 01:50
por zenildo » Sáb Jun 18, 2016 01:50
Adauto, tentei resolvê-la, porém não consegui. Tem como demonstrar como se resolve isto, pois tenho problemas em visualizar o que disse
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por adauto martins » Dom Jun 19, 2016 14:18
por adauto martins » Dom Jun 19, 2016 14:18
meu caro zenildo,
eu cometi um erro ai,e espero q. vc entenda a resoluçao:
prim. espero q. vc tenha entendido o ponto C(-1,0)da intersecçao do eixo-abscissas e pq o triang.
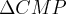
é isosceles...entao vamos á sol.correta:
tomando o

teremos:
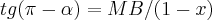
e
![MB=\sqrt[]{1-{(1-x)}^{2}} MB=\sqrt[]{1-{(1-x)}^{2}}](/latexrender/pictures/4a92363be3f661ba8b9950fa71b99f38.png)
,logo
![tg(\pi-\alpha)=-tg\alpha=\sqrt[]{1-{(1-x)}^{2}}/(1-x) tg(\pi-\alpha)=-tg\alpha=\sqrt[]{1-{(1-x)}^{2}}/(1-x)](/latexrender/pictures/8859129063dddefa5ac454130584debb.png)
...
![-tg\alpha=\sqrt[]{1-{(1-x)}^{2}/{(1-x)}^{2}}=\sqrt[]{1/{(1-x}^{2})-1}\Rightarrow {tg\alpha}^{2}=1/{(1-x)}^{2}-1 -tg\alpha=\sqrt[]{1-{(1-x)}^{2}/{(1-x)}^{2}}=\sqrt[]{1/{(1-x}^{2})-1}\Rightarrow {tg\alpha}^{2}=1/{(1-x)}^{2}-1](/latexrender/pictures/1c260b55ba4f302f93fe800138f819ea.png)
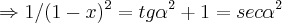
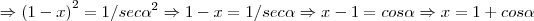
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Jun 19, 2016 14:27
por adauto martins » Dom Jun 19, 2016 14:27
eita outra correçao,é o latex,desculpe-me,erro mesmo:
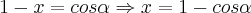
...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12992 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10973 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15115 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5031 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4795 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 em radianos. A distância do "início" do eixo x à esquerda até o M deve ser a mesma distância de M até P (pois a reta inclinada faz um ângulo de 45 graus). Assim sendo, é razoável concluir que a distância de M até P é
em radianos. A distância do "início" do eixo x à esquerda até o M deve ser a mesma distância de M até P (pois a reta inclinada faz um ângulo de 45 graus). Assim sendo, é razoável concluir que a distância de M até P é  , lembrando que este ciclo trigonométrico tem raio 1.
, lembrando que este ciclo trigonométrico tem raio 1.

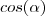 . Basta substituir.
. Basta substituir.
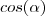 será negativo. Portanto, para a resposta ser o comprimento de M até P, é necessário mudar o sinal e o resultado fica
será negativo. Portanto, para a resposta ser o comprimento de M até P, é necessário mudar o sinal e o resultado fica 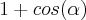 .
.

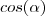 . Basta perceber que:
. Basta perceber que: , pois M0 é um comprimento que parte do ponto 0 no eixo dos cossenos e corresponde ao comprimento do arco.
, pois M0 é um comprimento que parte do ponto 0 no eixo dos cossenos e corresponde ao comprimento do arco.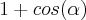 .
.




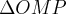 q.
q. 
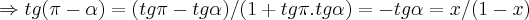
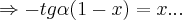 e ai é isolar o x,resolva o restante...
e ai é isolar o x,resolva o restante...

 é isosceles...entao vamos á sol.correta:
é isosceles...entao vamos á sol.correta: teremos:
teremos: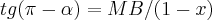 e
e ![MB=\sqrt[]{1-{(1-x)}^{2}} MB=\sqrt[]{1-{(1-x)}^{2}}](/latexrender/pictures/4a92363be3f661ba8b9950fa71b99f38.png) ,logo
,logo![tg(\pi-\alpha)=-tg\alpha=\sqrt[]{1-{(1-x)}^{2}}/(1-x) tg(\pi-\alpha)=-tg\alpha=\sqrt[]{1-{(1-x)}^{2}}/(1-x)](/latexrender/pictures/8859129063dddefa5ac454130584debb.png) ...
...![-tg\alpha=\sqrt[]{1-{(1-x)}^{2}/{(1-x)}^{2}}=\sqrt[]{1/{(1-x}^{2})-1}\Rightarrow {tg\alpha}^{2}=1/{(1-x)}^{2}-1 -tg\alpha=\sqrt[]{1-{(1-x)}^{2}/{(1-x)}^{2}}=\sqrt[]{1/{(1-x}^{2})-1}\Rightarrow {tg\alpha}^{2}=1/{(1-x)}^{2}-1](/latexrender/pictures/1c260b55ba4f302f93fe800138f819ea.png)
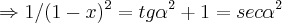
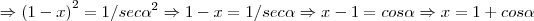 ...
...
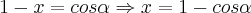 ...obrigado
...obrigado