 por holandaleo » Sáb Fev 13, 2016 18:48
por holandaleo » Sáb Fev 13, 2016 18:48
Olá a todos, alguém pode me ajudar com a resolução dessa questão que envolve PIF?
-Demonstrar a seguinte preposição;
![x+{x}^{2}+{x}^{3}+{x}^{4}...{x}^{n}=\frac{{1-x}^{n+1}}{1-x}[para ] n\geq1,x\neq1 x+{x}^{2}+{x}^{3}+{x}^{4}...{x}^{n}=\frac{{1-x}^{n+1}}{1-x}[para ] n\geq1,x\neq1](/latexrender/pictures/4cd36ba7ea11c4173a643e098f89659c.png)
-
holandaleo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Fev 13, 2016 18:25
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por adauto martins » Qui Fev 25, 2016 21:31
por adauto martins » Qui Fev 25, 2016 21:31
soma dos termos de uma PG finita de razao,q=x...
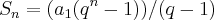
...a questao apresentada nao esta correta,pois:
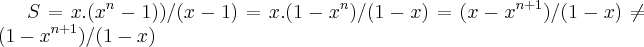
...
logo
![S=x+{x}^{2}+...+{x}^{n}=x.(1-{x}^{n+1})/(1-x),p/x\neq 1,[\tex] S=x+{x}^{2}+...+{x}^{n}=x.(1-{x}^{n+1})/(1-x),p/x\neq 1,[\tex]](/latexrender/pictures/908bc32ecd93cae8840167fa65b2a95a.png)
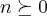
...vamos á prova por induçao...
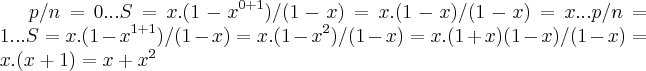
...
vamos supor p/

, ou seja
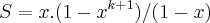
verdadeira...entao...
p/

,teriamos...
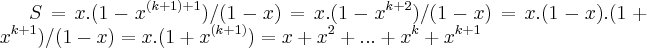
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Indução finita !
 por Lucas Alves Ribeiro » Dom Mar 10, 2013 22:47
por Lucas Alves Ribeiro » Dom Mar 10, 2013 22:47
- 0 Respostas
- 1218 Exibições
- Última mensagem por Lucas Alves Ribeiro

Dom Mar 10, 2013 22:47
Álgebra Elementar
-
- Princípio da Indução Finita
por Fontelles » Dom Jan 17, 2010 14:42
- 9 Respostas
- 105769 Exibições
- Última mensagem por Vennom

Qui Abr 26, 2012 23:04
Funções
-
- PIF - Principio da Indução Finita
por ederj » Seg Jun 28, 2010 13:35
- 3 Respostas
- 8058 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 20:01
Funções
-
- Álgebra: Indução Finita
por Caeros » Ter Mar 08, 2011 13:13
- 6 Respostas
- 4055 Exibições
- Última mensagem por MarceloFantini

Ter Mar 08, 2011 21:44
Álgebra Elementar
-
- Indução Finita FIbonacci
por Garota nerd » Ter Mai 03, 2011 17:52
- 3 Respostas
- 2966 Exibições
- Última mensagem por Garota nerd

Qui Mai 05, 2011 00:43
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x+{x}^{2}+{x}^{3}+{x}^{4}...{x}^{n}=\frac{{1-x}^{n+1}}{1-x}[para ] n\geq1,x\neq1 x+{x}^{2}+{x}^{3}+{x}^{4}...{x}^{n}=\frac{{1-x}^{n+1}}{1-x}[para ] n\geq1,x\neq1](/latexrender/pictures/4cd36ba7ea11c4173a643e098f89659c.png)

![x+{x}^{2}+{x}^{3}+{x}^{4}...{x}^{n}=\frac{{1-x}^{n+1}}{1-x}[para ] n\geq1,x\neq1 x+{x}^{2}+{x}^{3}+{x}^{4}...{x}^{n}=\frac{{1-x}^{n+1}}{1-x}[para ] n\geq1,x\neq1](/latexrender/pictures/4cd36ba7ea11c4173a643e098f89659c.png)

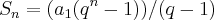 ...a questao apresentada nao esta correta,pois:
...a questao apresentada nao esta correta,pois: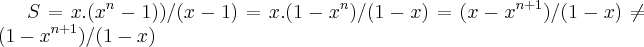 ...
...![S=x+{x}^{2}+...+{x}^{n}=x.(1-{x}^{n+1})/(1-x),p/x\neq 1,[\tex] S=x+{x}^{2}+...+{x}^{n}=x.(1-{x}^{n+1})/(1-x),p/x\neq 1,[\tex]](/latexrender/pictures/908bc32ecd93cae8840167fa65b2a95a.png)
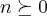 ...vamos á prova por induçao...
...vamos á prova por induçao...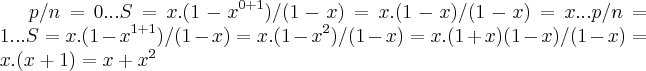 ...
... , ou seja
, ou seja 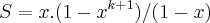 verdadeira...entao...
verdadeira...entao... ,teriamos...
,teriamos...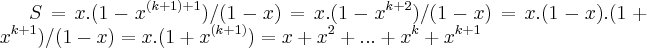

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.