Alguém poderia me ajudar nesta questão, por favor?
Em uma empresa, o salário médio era de R$ 3.000,00, e o desvio padrão dos salários era de R$ 300,00. Todos os funcionários receberam um aumento de 10%. A variância dos salários ficou aumentada em:
(A) 5%. (B) 10%. (C) 11%. (D) 21%. (E) 121%
Eu cheguei ao resultado de 10% (alternativa B), mas o gabarito consta como correto a alternativa (E) 121%
Agradeço desde já!


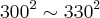
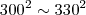
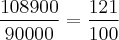


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.