 0. O custo de produção é de C(x)= 500 + 15x +
0. O custo de produção é de C(x)= 500 + 15x + 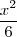 unidades monetárias. Determine x para que o lucro
unidades monetárias. Determine x para que o lucro( = venda - custo ) seja máximo. Determine, também, o lucro máximo.
Gabarito: x= 30 toneladas . Lucro = 1150 unidades monetárias
Entao, eu comecei tentando descobrir a função da venda isolando o p na função que ele da relacionada, depois eu faço a função do lucro que seria a
função p - a função custo ( C(x) ). Depois eu derivei essa função lucro descoberto e igualei a zero pra achar o ponto crítico.
O meu problema que esse x que eu encontro nunca é igual do gabarito, eu nao sei se é erro de calculo ou a abordagem que fiz ta errada ou o próprio gabarito estar errado. Serei muito grato se alguem pudesse me ajudar :]


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)