Consegui chegar até na metade deste exercício e gostaria da ajuda de vocês para termina-lo.
Ex. Mostrar que a função y =
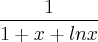satisfaz a equação xy' = y (y ln x - 1).Até onde consegui fazer:
y =
=
=
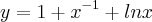
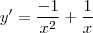
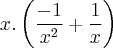
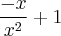
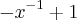isso tem que ser = y (y ln x - 1).Depois disso eu empaquei e não consegui igualar com essa parte: y (y ln x - 1).
Por favor vejam se meu raciocínio esta certo, me ajudem!! preciso entregar isso no final da semana que vem, obrigado desde já!
.
