 por Fabio Ribeiro » Qui Jun 05, 2014 12:30
por Fabio Ribeiro » Qui Jun 05, 2014 12:30
Olá!
Estou resolvendo uma função de terceiro grau. Preciso descobrir qual o valor de máximo relativo dessa função. Nos meus cálculos cheguei ao ponto crítico x=7, porém não consigo achar o valor correto de y. Sei que a resposta é aproximadamente 150, mas não consigo chegar a esse resultado. Nas minhas tentativas sempre chego em aproximadamente 110. Gostaria de um apoio de vocês para saber onde estou errando.
Eis a função:
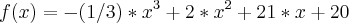
Quando

Sei que a resposta correta é aproximadamente 150, mas só consigo chegar em um resultado de aproximadamente 110. Provavelmente estou errando na álgebra. Preciso de um apoio para saber onde estou errando, pois não consigo chegar no valor correto.
Obrigado!
-
Fabio Ribeiro
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 05, 2014 12:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Automação Industrial
- Andamento: formado
 por blaze » Sex Jun 06, 2014 10:23
por blaze » Sex Jun 06, 2014 10:23
É bem simples. Fazes a derivada dessa função e igualas a 0; vai-te dar 7 e -3 como solução. Fazes um quadro de sinal e vês que 7 é o máximo e -3 o mínimo.
Como já chegaste a estas contas não me vou dar ao trabalho de as pôr aqui.
Então, é só substituir 7 na função dada, que dá 150 mais 2/3, que é aproximadamente 150.
O que deves ter feito, e erradamente como é óbvio, foi por tudo na calculadora e ela que faça a conta. Faz parcela a parcela que vais ver que tens o mesmo resultado que eu
-
blaze
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 07, 2014 17:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabio Ribeiro » Sex Jun 06, 2014 16:25
por Fabio Ribeiro » Sex Jun 06, 2014 16:25
Blaze, obrigado pela atenção e pela resposta!
Venho tentando passo a passo encontrar a solução, mas sempre encontro um valor de aproximadamente 110,67 conforme mencionado anteriormente.
Eis minha resolução (errada):
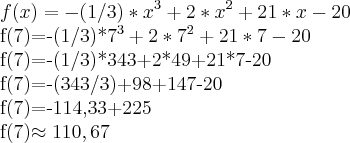
Creio que seja simples, mas não estou conseguindo visualizar o meu erro. Onde está esse erro?
Novamente, obrigado pela ajuda e pela atenção!
-
Fabio Ribeiro
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 05, 2014 12:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Automação Industrial
- Andamento: formado
 por blaze » Sex Jun 06, 2014 21:08
por blaze » Sex Jun 06, 2014 21:08
De onde veio esse -20?
Atenção aos erros de sinais!
-
blaze
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 07, 2014 17:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabio Ribeiro » Sáb Jun 07, 2014 18:56
por Fabio Ribeiro » Sáb Jun 07, 2014 18:56
Obrigado pelo alerta!
Eu vinha errando consecutivamente esse sinal e realmente não notava!
Muito obrigado pela ajuda!
Abraço!
-
Fabio Ribeiro
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 05, 2014 12:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Automação Industrial
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- maximo e minimos relativo
por matematica_mat » Sáb Out 29, 2011 13:05
- 0 Respostas
- 1740 Exibições
- Última mensagem por matematica_mat

Sáb Out 29, 2011 13:05
Cálculo Numérico e Aplicações
-
- Diferenciais - Erro máximo e relativo
por Vencill » Ter Dez 02, 2014 17:21
- 2 Respostas
- 13684 Exibições
- Última mensagem por Vencill

Qua Dez 03, 2014 16:22
Cálculo: Limites, Derivadas e Integrais
-
- (Equação de 2° grau) com o Delta sem valor exato
por morcego265 » Sáb Jul 27, 2013 13:48
- 1 Respostas
- 1523 Exibições
- Última mensagem por DanielFerreira

Sáb Ago 03, 2013 08:48
Equações
-
- [Valor máximo de função]
por alicemneves » Seg Mai 28, 2012 11:39
- 1 Respostas
- 1602 Exibições
- Última mensagem por Russman

Seg Mai 28, 2012 18:31
Funções
-
- [Encontrar valor A, B e C]
por engrobson » Dom Out 06, 2013 17:14
- 0 Respostas
- 1292 Exibições
- Última mensagem por engrobson

Dom Out 06, 2013 17:14
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
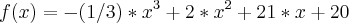



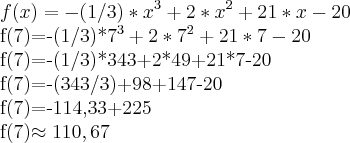
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
