 por Mario_Mascarenhas » Sáb Mar 22, 2014 17:52
por Mario_Mascarenhas » Sáb Mar 22, 2014 17:52
Olá, pessoal.
Estou com dificuldade para isolar o X em uma questão.
(B.A^t)^t.X.B.A^t = 4A.A^t + C.X.B.A^t
O professor isolou o x e ficou assim. Não entendi de que modo ele chegou a isso:
X = [(B.A^t)^t - C]^-1 . 4A.A^t . (B.A^t)^-1
Alguém poderia me explicar, detalhadamente?
Obrigado.
Obs.: o " ^t " significa matriz transposta.
-
Mario_Mascarenhas
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 22, 2014 17:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Seg Mar 24, 2014 01:12
por e8group » Seg Mar 24, 2014 01:12
Boa noite !
Só para simplificar vou considerar
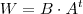
e escrever a eq.matricial como
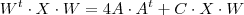
ou
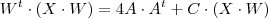
ou ainda
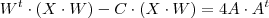
Agora observe que deixando a matriz entre parêntesis em evidência , temos
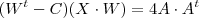
(Se aplicar a distributiva chegará na mesma eq. acima)
Para isolar

, a matriz
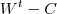
e

devem ser invertíveis . Daí é só multiplicar ambos os membros por
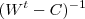
(pela esquerda) e
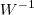
(pela direita) .
Isto é ,
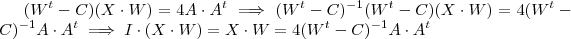
. Agora é só fazer a segunda etapa e dps subst. W por B \cdot A^t .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação matricial envolvendo matriz inversa] Como isolar X?
por Mario_Mascarenhas » Sáb Mar 22, 2014 17:52
- 0 Respostas
- 1775 Exibições
- Última mensagem por Mario_Mascarenhas

Sáb Mar 22, 2014 17:52
Álgebra Linear
-
- Determinar a matriz X na Equação matricial AX=B
por hugo guedes » Qui Mar 12, 2015 10:37
- 1 Respostas
- 24062 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 25, 2015 16:58
Matrizes e Determinantes
-
- Determinar a matriz X na Equação matricial AX=B
por hugo guedes » Qui Mar 12, 2015 12:16
- 1 Respostas
- 4388 Exibições
- Última mensagem por andrerodrigues98

Qui Mar 12, 2015 15:25
Matrizes e Determinantes
-
- Como isolar PV nesta equação
por macburn » Qua Dez 15, 2010 20:22
- 1 Respostas
- 1487 Exibições
- Última mensagem por Bruno Pinheiro

Dom Dez 26, 2010 23:10
Logaritmos
-
- Como calcular o determinante inversa da Matriz ?
por gustavosec » Sáb Mar 26, 2016 16:55
- 1 Respostas
- 16162 Exibições
- Última mensagem por vitor_jo

Sáb Jul 16, 2016 03:17
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


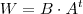 e escrever a eq.matricial como
e escrever a eq.matricial como 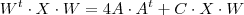
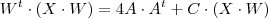
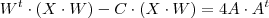
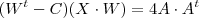 (Se aplicar a distributiva chegará na mesma eq. acima)
(Se aplicar a distributiva chegará na mesma eq. acima)  , a matriz
, a matriz 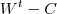 e
e  devem ser invertíveis . Daí é só multiplicar ambos os membros por
devem ser invertíveis . Daí é só multiplicar ambos os membros por 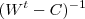 (pela esquerda) e
(pela esquerda) e 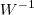 (pela direita) .
(pela direita) . 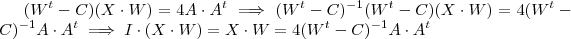 . Agora é só fazer a segunda etapa e dps subst. W por B \cdot A^t .
. Agora é só fazer a segunda etapa e dps subst. W por B \cdot A^t .