 por pam_nivens » Sáb Nov 28, 2009 21:26
por pam_nivens » Sáb Nov 28, 2009 21:26
Bem... eu fiz vários exercícios de integral indefinida e estava indo muito bem.
Cheguei em método da substituição e resolvi os primeiros exercícios até não entender por q o meu u estava dando diferente
no caso na seguinte integral :
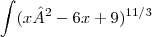
dx (IGNOREM A LETRA A NA FÓRMULA, NÃO CONSEGUI TIRAR! É X ELEVADO AO QUADRADO) o meu problema deu u = x-3 no gabarito e resposta : -3/x -5/3x³ +c . Eu não enntendi por q o u é = a x-3 . Me ajudem por favor, tenho prova segunda !!!!!
-
pam_nivens
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 26, 2009 17:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia UFF
- Andamento: cursando
 por marciommuniz » Dom Nov 29, 2009 00:58
por marciommuniz » Dom Nov 29, 2009 00:58
Olá, não sei se entendi muito bem seu problema..
mas lembre-se
x²-6x+9 = (x-3)²
Arrumando a integral...
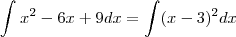
fazendo u=x-3
![\int{(x^2-6x+9)}^{11/3}dx=\int[{(x-3)}^2]^{11/3}dx = \int{(u)}^{2*11/3}dx \int{(x^2-6x+9)}^{11/3}dx=\int[{(x-3)}^2]^{11/3}dx = \int{(u)}^{2*11/3}dx](/latexrender/pictures/e8d9d109dcdfdc24d4308b3f715e2909.png)
=
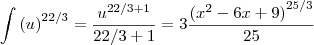
+C
Acho que é isso, não sei se me confundi.
Vlw!
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mudança de Variável
por DanielFerreira » Dom Abr 22, 2012 13:58
- 2 Respostas
- 1611 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de Variável
 por DanielFerreira » Dom Abr 29, 2012 21:06
por DanielFerreira » Dom Abr 29, 2012 21:06
- 3 Respostas
- 1885 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 15:56
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variavel na integral
por matmatco » Ter Abr 23, 2013 22:29
- 0 Respostas
- 1125 Exibições
- Última mensagem por matmatco

Ter Abr 23, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variável em exercício de integração
por Skyliner » Qua Nov 25, 2009 23:02
- 2 Respostas
- 3475 Exibições
- Última mensagem por Skyliner

Qui Nov 26, 2009 01:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Mudança de variável
por VFernandes » Ter Jan 03, 2012 23:47
- 2 Respostas
- 2145 Exibições
- Última mensagem por VFernandes

Qui Jan 05, 2012 23:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
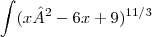 dx (IGNOREM A LETRA A NA FÓRMULA, NÃO CONSEGUI TIRAR! É X ELEVADO AO QUADRADO) o meu problema deu u = x-3 no gabarito e resposta : -3/x -5/3x³ +c . Eu não enntendi por q o u é = a x-3 . Me ajudem por favor, tenho prova segunda !!!!!
dx (IGNOREM A LETRA A NA FÓRMULA, NÃO CONSEGUI TIRAR! É X ELEVADO AO QUADRADO) o meu problema deu u = x-3 no gabarito e resposta : -3/x -5/3x³ +c . Eu não enntendi por q o u é = a x-3 . Me ajudem por favor, tenho prova segunda !!!!!

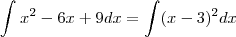
![\int{(x^2-6x+9)}^{11/3}dx=\int[{(x-3)}^2]^{11/3}dx = \int{(u)}^{2*11/3}dx \int{(x^2-6x+9)}^{11/3}dx=\int[{(x-3)}^2]^{11/3}dx = \int{(u)}^{2*11/3}dx](/latexrender/pictures/e8d9d109dcdfdc24d4308b3f715e2909.png)
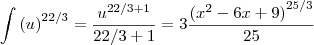 +C
+C


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.