 por luiz1903 » Seg Fev 10, 2014 17:51
por luiz1903 » Seg Fev 10, 2014 17:51
Boa tarde a todos, sou novo no fórum e gostaria de tirar umas dúvidas. A questão pede para vc dizer se a série converge ou diverge usando o teste da comparação. Teve tres questões que eu não consegui fazer:
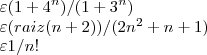
Sempre o somatório de n=1 até infinito.
Obrigado
-
luiz1903
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 10, 2014 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
 por e8group » Seg Fev 10, 2014 20:41
por e8group » Seg Fev 10, 2014 20:41
Boa noite . O que você tentou , quais as dúvidas ?
A primeira pode compara com a série de termos constantes iguais a 1 (pois ,
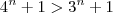
, para todo n) .
Na terceira , para qualquer
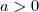
fixado , sempre
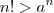
para

suficientemente grande .
Basta fixar qualquer

e comparar a série
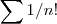
com a geométrica \sum (1/a)^n [/tex] .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por luiz1903 » Ter Fev 11, 2014 09:57
por luiz1903 » Ter Fev 11, 2014 09:57
Obrigado por responder.
Na primeira eu peguei a série (6/5)^n, q é uma serie divergente e tem sempre bn<an (an é a série estudada). Sendo assim, an é divergente. Isso está correto?
Não entendi pq vc disse q n!>2^n. Eu preciso de uma série onde bn>an. Supondo a série 1/2^n, os primeiros termos dessa série serão 1/2, 1/4, 1/8... enquanto que os primeiros termos da série 1/n! serão 1/1, 1/2, 1/6 de forma que bn<an
-
luiz1903
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 10, 2014 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
 por e8group » Ter Fev 11, 2014 17:33
por e8group » Ter Fev 11, 2014 17:33
Observe que se
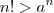
, isto automaticamente implica
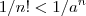
(em geral para n suficientemente grande , entretanto , para caso particulares , como

por exemplo .Neste caso basta impor que
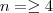
) .
Complementando , se a série
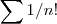
converge
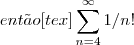
também converge .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [SÉRIE] teste de comparação para convergência
por magellanicLMC » Ter Jan 28, 2014 20:47
- 5 Respostas
- 5332 Exibições
- Última mensagem por e8group

Sáb Fev 01, 2014 19:03
Sequências
-
- [SÉRIE] teste da integral
por magellanicLMC » Qua Fev 05, 2014 20:38
- 1 Respostas
- 1788 Exibições
- Última mensagem por e8group

Qui Fev 06, 2014 11:55
Cálculo: Limites, Derivadas e Integrais
-
- Duvida de Série pelo teste da integral
por douglasnickson » Sáb Ago 20, 2016 13:41
- 0 Respostas
- 4071 Exibições
- Última mensagem por douglasnickson

Sáb Ago 20, 2016 13:41
Sequências
-
- [Série] Calcular valor de série tendo outra como referência
por robmenas » Dom Abr 07, 2019 14:35
- 0 Respostas
- 9189 Exibições
- Última mensagem por robmenas

Dom Abr 07, 2019 14:35
Sequências
-
- [série de Euler / problema da Basiléia] Série de Fourier
por Burnys » Qua Jul 16, 2008 14:34
- 4 Respostas
- 9084 Exibições
- Última mensagem por admin

Qui Jul 17, 2008 00:33
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
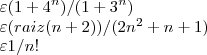

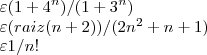

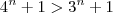 , para todo n) .
, para todo n) . 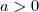 fixado , sempre
fixado , sempre 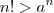 para
para  suficientemente grande .
suficientemente grande .  e comparar a série
e comparar a série 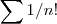 com a geométrica \sum (1/a)^n [/tex] .
com a geométrica \sum (1/a)^n [/tex] .

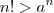 , isto automaticamente implica
, isto automaticamente implica 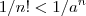 (em geral para n suficientemente grande , entretanto , para caso particulares , como
(em geral para n suficientemente grande , entretanto , para caso particulares , como  por exemplo .Neste caso basta impor que
por exemplo .Neste caso basta impor que 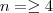 ) .
) .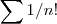 converge
converge 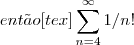 também converge .
também converge .


 , avisa que eu resolvo.
, avisa que eu resolvo.

