Por que a minha resolução do seguinte exercício está errada?
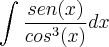
Pelo Teorema da Mudança de Variável, temos:
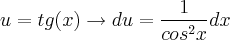
Daí,
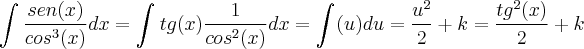
Obrigada!

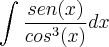
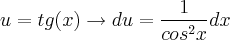
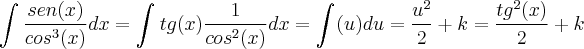



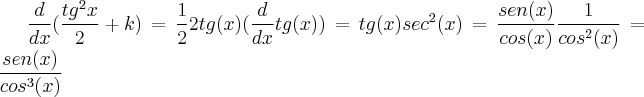




Pessoa Estranha escreveu:Olá, pessoal!
Por que a minha resolução do seguinte exercício está errada?
Pelo Teorema da Mudança de Variável, temos:
Daí,
Obrigada!
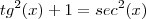

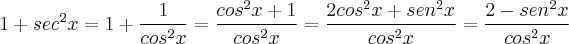


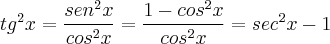

Pessoa Estranha escreveu:
Olha, se eu não errei nas manipulações, o certo não é assim?



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: