[ Em uma empresa telefônica, 17 em cada 20 clientes utilizam o sistema pré - pago. Sendo assim, o número de clientes que utilizam o sistema pré-pago supera o número de clientes do pós-pago em 24,36 milhões. Quantos milhões de clientes são atendidos por essa empresa?
(A) 29,58 (B) 30,25 (C) 31,20 (D) 32,18 (E) 34,80
Descobri que a diferença é de 85% , estou tentando o seguinte raciocínio x+(85%x)=24,36


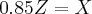
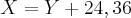
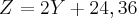
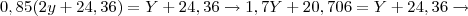
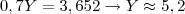
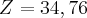 . (Aproximado).
. (Aproximado).

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
