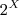 x
x 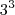 x
x 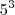 x 7.
x 7. Sendo A =
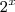 x
x 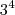 x
x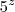 x 7 e B =
x 7 e B =  x
x 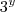 x
x 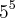 x 7, então o valor de produto xyz é:
x 7, então o valor de produto xyz é:a)20 b)80 c)60 d)40 e)11
Entendi esse exercício até determinada parte: para saber o mdc entre dois números, quando fatorados em separado, devo utilizar os fatores comuns com os menores expoentes, portanto, ficou fácil descobrir y = 3 e z = 4.
A partir de agora não sabia mais o que fazer para descobrir o x, então verifiquei a resolução do problema, que explica que basta perceber que a resposta é um múltiplo de 12 (4 x 3=12), portanto, a alternativa correta seria a C.
Mas não sei qual raciocínio preciso seguir para entender que simplesmente devo multiplicar os dois expoentes descobertos, 4 e 3, para dizer que o 12 deve ser múltiplo do resultado, sendo que há mais um fator que não descobri.
Se necessário, segue o link do problema, é o número 07: http://www.matematicamuitofacil.com/mdc01.html


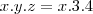
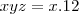


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.