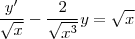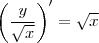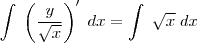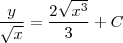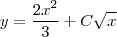por kayone » Dom Set 22, 2013 17:37
por kayone » Dom Set 22, 2013 17:37
Pessoal boa tarde, estamos com um grupo de estudos e encontramos o seguinte problema que nenhum de nós conseguimos resolver.
Seria a seguinte equação:
y'= x+y/2x
chegamos em:
dy = xdx
y 2x
Então:
lny = ??? agora travamos...alguem pode ajudar ? Obrigado
-
kayone
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Set 22, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Man Utd » Dom Jun 15, 2014 23:49
por Man Utd » Dom Jun 15, 2014 23:49
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Solução de uma Equação diferencial ordinaria
por thejotta » Seg Jan 14, 2013 00:03
- 0 Respostas
- 1024 Exibições
- Última mensagem por thejotta

Seg Jan 14, 2013 00:03
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial] Solução incorreta?
por KleinIll » Qui Set 19, 2013 15:45
- 2 Respostas
- 1713 Exibições
- Última mensagem por KleinIll

Sáb Set 21, 2013 01:15
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial parcial] Ajuda para solução de EDP
por GustavoArtur » Qui Set 22, 2011 14:24
- 3 Respostas
- 2538 Exibições
- Última mensagem por GustavoArtur

Sex Set 23, 2011 12:58
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial] Região no plano com única solução
por Aliocha Karamazov » Dom Fev 26, 2012 11:52
- 1 Respostas
- 3788 Exibições
- Última mensagem por LuizAquino

Dom Fev 26, 2012 13:39
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais: solução geral
por emsbp » Sáb Abr 07, 2012 18:01
- 1 Respostas
- 892 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 07, 2012 19:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


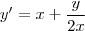
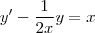
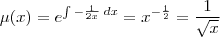 , multiplique toda a equação por esse fator :
, multiplique toda a equação por esse fator :