-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 481074 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 543635 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 507407 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 738460 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2186808 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por krtc » Qua Jul 24, 2013 02:07
por krtc » Qua Jul 24, 2013 02:07
Estou com dúvidas neste exercício:
Seja R a região limitada pela parábola

, pela reta y = 2x – 1 e pelo eixo x. Encontre o valor da área R.
Não sei se é pra calcular apenas a área acima do eixo x ou abaixo...pois a reta passa por -1 no eixo y e é tangente a parábola no ponto (1,1)...
Desde já, agradeço quem ajudar.
-
krtc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 24, 2013 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 02:19
por Russman » Qua Jul 24, 2013 02:19
Ele quer que você calcule a areazinha em forma "quase" triangular, alí.
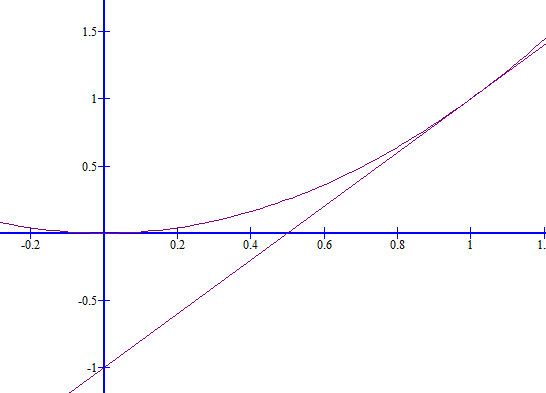
- graph
- graph (2).gif (3.96 KiB) Exibido 3344 vezes
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por krtc » Qua Jul 24, 2013 02:34
por krtc » Qua Jul 24, 2013 02:34
Russman escreveu:Ele quer que você calcule a areazinha em forma "quase" triangular, alí.
graph (2).gif
Ele quer que você calcule a areazinha em forma "quase" triangular, alí.
graph (2).gif
[/quote]
Então eu preciso calcular em função do y?
fazer
![x=\sqrt[]{y} x=\sqrt[]{y}](/latexrender/pictures/371065f56f4fad1c22d082bb674a29e1.png)
e
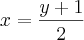
, ficando
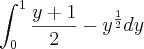
...tá certo o q eu fiz ou fiz besteira?
o resultado deu "
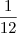
"
-
krtc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 24, 2013 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 02:48
por Russman » Qua Jul 24, 2013 02:48
Pode fazer assim como tu fez, pq se deu
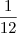
deve estar certo.
Eu faria a integral

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por krtc » Qua Jul 24, 2013 02:54
por krtc » Qua Jul 24, 2013 02:54
Russman escreveu:Pode fazer assim como tu fez, pq se deu
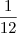
deve estar certo.
Eu faria a integral

Entendi! Eu pegava o intervalo errado para a reta!
Muito obrigado Russman!
-
krtc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 24, 2013 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 03:13
por Russman » Qua Jul 24, 2013 03:13
Não, na integral em y o intervalo é de 0 à 1. Você fez certo. Só errou o sinal na integral que você postou.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4033 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 1892 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2646 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2720 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Area
por karenblond » Qui Mar 25, 2010 17:19
- 6 Respostas
- 3738 Exibições
- Última mensagem por Molina

Ter Mar 30, 2010 00:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , pela reta y = 2x – 1 e pelo eixo x. Encontre o valor da área R.
, pela reta y = 2x – 1 e pelo eixo x. Encontre o valor da área R.


![x=\sqrt[]{y} x=\sqrt[]{y}](/latexrender/pictures/371065f56f4fad1c22d082bb674a29e1.png) e
e 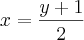 , ficando
, ficando 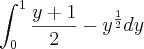 ...tá certo o q eu fiz ou fiz besteira?
...tá certo o q eu fiz ou fiz besteira?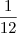 "
"
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
