Se
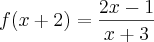 ,
, 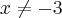 , o domínio de f(x) é:
, o domínio de f(x) é:a) R
b) R*
c) {
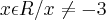
d)
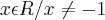
e)
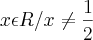
Resolução
g(x)=x+2 -> f(y) -> y=x+2
![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)
Parei aí... não consigo terminar pois não sei como acha a restrição para o numerador! Me ajude por favor...

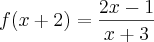 ,
, 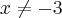 , o domínio de f(x) é:
, o domínio de f(x) é: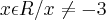
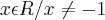
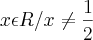
![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)



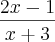 , a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.
, a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)