 por junior oliveira » Sex Jun 14, 2013 17:07
por junior oliveira » Sex Jun 14, 2013 17:07
Dizemos que uma matriz A é simétrica se A^t = A e que A é antissimétrica se
At = -A. Mostre que
a. Se Amxn é uma matriz qualquer, então as matrizes Bnxn = A^t.A e Cmm = AA^t
são simétricas;
b. Se A é uma matriz quadrada de ordem n, então as matrizes B = 1/2(A+A^t)
e C = 1/2 (A - At) são, respectivamente, simétrica e antissimétrica;
c. Usando o item anterior, mostre que toda matriz pode ser escrita de forma única
como soma de uma matriz simétrica com uma antissimétrica;
d. Mostre que a única matriz que é, simultaneamente, simétrica e antissimétrica é a
matriz nula.
passo a passo em gente, valeu
-
junior oliveira
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 30, 2013 08:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic.fisica
- Andamento: cursando
 por e8group » Sex Jun 14, 2013 20:15
por e8group » Sex Jun 14, 2013 20:15
O que você tentou ?
(a) Deve mostrar que
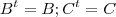
.Para isto,note que :
![[A^t\cdot A]_{ij} = \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} [A^t\cdot A]_{ij} = \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj}](/latexrender/pictures/f108168f9d4df5673530f4f462b6b77f.png)
para todo
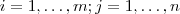
. Observando ,
![[A^t]_{ik}[A]_{kj} = [A]_{ki}[A^t]_{jk} [A^t]_{ik}[A]_{kj} = [A]_{ki}[A^t]_{jk}](/latexrender/pictures/660fa1091567d5c3807c75893228054b.png)
e como produtos de números são comutativos ,você pode concluir que
![[A]_{ki}[A^t]_{jk} = [A^t]_{jk} \cdot [A]_{ki} [A]_{ki}[A^t]_{jk} = [A^t]_{jk} \cdot [A]_{ki}](/latexrender/pictures/31a67968d4ed6e8bf773379b07d93225.png)
.Logo ,
![\sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} = \sum_{k=1}^{n}[A^t]_{jk} \cdot [A]_{ki} = [B]_{ji} \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} = \sum_{k=1}^{n}[A^t]_{jk} \cdot [A]_{ki} = [B]_{ji}](/latexrender/pictures/33b2a968c89c731ca3bbf51df6a69715.png)
para todo
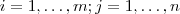
. A outra questão é análoga .
(b) Basta utilizar a comutatividade da adição e comparar o resultado com
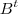
e na outra matriz ,evidencie

e compare com
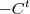
.
(c) Basta somar elas e mostrar que se pede no enunciado .
(d) Seja
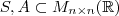
,respectivamente ,o conjunto das matrizes simétricas e anti-simétricas .Basta mostra que
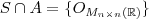
. Onde :
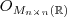
é o vetor nulo do conjunto das matrizes

.
Comente as dúvidas .
Observação :Post apenas uma dúvida por tópico na próxima vez ,certo ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8159 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10534 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11566 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13607 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9152 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


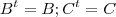 .Para isto,note que :
.Para isto,note que : ![[A^t\cdot A]_{ij} = \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} [A^t\cdot A]_{ij} = \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj}](/latexrender/pictures/f108168f9d4df5673530f4f462b6b77f.png) para todo
para todo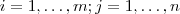 . Observando ,
. Observando , ![[A^t]_{ik}[A]_{kj} = [A]_{ki}[A^t]_{jk} [A^t]_{ik}[A]_{kj} = [A]_{ki}[A^t]_{jk}](/latexrender/pictures/660fa1091567d5c3807c75893228054b.png) e como produtos de números são comutativos ,você pode concluir que
e como produtos de números são comutativos ,você pode concluir que ![[A]_{ki}[A^t]_{jk} = [A^t]_{jk} \cdot [A]_{ki} [A]_{ki}[A^t]_{jk} = [A^t]_{jk} \cdot [A]_{ki}](/latexrender/pictures/31a67968d4ed6e8bf773379b07d93225.png) .Logo ,
.Logo , ![\sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} = \sum_{k=1}^{n}[A^t]_{jk} \cdot [A]_{ki} = [B]_{ji} \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} = \sum_{k=1}^{n}[A^t]_{jk} \cdot [A]_{ki} = [B]_{ji}](/latexrender/pictures/33b2a968c89c731ca3bbf51df6a69715.png) para todo
para todo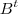 e na outra matriz ,evidencie
e na outra matriz ,evidencie  e compare com
e compare com 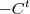 .
. 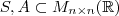 ,respectivamente ,o conjunto das matrizes simétricas e anti-simétricas .Basta mostra que
,respectivamente ,o conjunto das matrizes simétricas e anti-simétricas .Basta mostra que 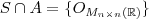 . Onde :
. Onde : 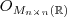 é o vetor nulo do conjunto das matrizes
é o vetor nulo do conjunto das matrizes  .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.