 por sanleovig » Seg Mai 06, 2013 15:19
por sanleovig » Seg Mai 06, 2013 15:19
A final do Campeonato Paulista de Futebol de 1973 entre Santos e Portuguesa foi decidida nos pênaltis. Após a cobrança de 3 pênaltis por cada time (de um total de 5), o placar estava 2x0 para o Santos quando o árbitro terminou o jogo. Porém, a Portuguesa poderia acertar os dois pênaltis que lhe restavam e o Santos errar seus dois, o que resultaria em empate.
Para compensar o erro, a Federação Paulista de Futebol declarou os dois times campeões nesse ano.
Mas será que essa decisão foi a mais justa?
a) Considerando que a probabilidade de um jogador marcar o gol na cobrança de um pênalti é 50%, qual era a chance de a Portuguesa conseguir empatar a cobrança de pênaltis?
b) De acordo com a FIFA (baseando-se em cobranças de pênalti em jogos oficiais) a probabilidade de um jogador que irá cobrar o pênalti marcar o gol é de 80%. Nesse caso, qual era a probabilidade de a Portuguesa conseguir empatar a cobrança de pênaltis?
Eu resolví desta forma:
Chamando de (e) a probabilidade de empate, (A) as chances de acertar e (E) as chances de errar, temos:
a) P(e) = (AA) / (EEAA) -> P(A) = 2 / 4 -> P(A) = 1 / 2 -> P(A) = 50%
b) Como a probabilidade de acerto representa 80% sobram 20% para erro, então temos:
P(e) = (AA) / (EEAA) -> P(A) = 160 / 200 -> P(e) = 80%
Este meu raciocínio procede?
-
sanleovig
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 05, 2013 19:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por brunoiria » Sex Mai 10, 2013 14:07
por brunoiria » Sex Mai 10, 2013 14:07
Ola sanleovig,
eu pensei deste modo
Sendo B= os penaltis restantes par ambas equipes, e A=conversam dos penaltis da portuguesa e erro do santos.
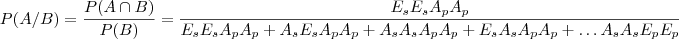
aqui vc terá que analisar todas as 16 combinações possíveis. como as chances de acerto e erro são iguais cada uma delas é de
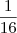
. assim
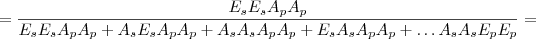
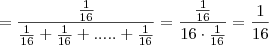
na b) vc terá que tomar cuidado pois a prob de acerto não é igual a do erro, mas acho que resolve do mesmo modo que aqui. um livro para consulta pode ser do morgado "probabilidade e análise combinatória" editora sbm, de uma olhada nele. boa sorte
-
brunoiria
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Jun 23, 2012 10:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic Mat
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade - jogo de futebol]
por etocda » Ter Mar 12, 2013 21:30
- 4 Respostas
- 9369 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 17:36
Probabilidade
-
- Probabilidade no jogo de Poker
por jlmanetti » Sáb Out 10, 2009 22:42
- 2 Respostas
- 3554 Exibições
- Última mensagem por jlmanetti

Seg Out 12, 2009 12:47
Estatística
-
- [PROBABILIDADE] Jogo de Dados
por sweelinck » Qua Nov 23, 2011 02:47
- 3 Respostas
- 3407 Exibições
- Última mensagem por MarceloFantini

Qua Nov 23, 2011 16:35
Estatística
-
- [Probabilidade condicionada] Jogo de dados
por llbranco » Qui Abr 09, 2015 02:18
- 0 Respostas
- 2687 Exibições
- Última mensagem por llbranco

Qui Abr 09, 2015 02:18
Probabilidade
-
- problema do futebol
por hevhoram » Qui Jul 18, 2013 11:49
- 1 Respostas
- 13458 Exibições
- Última mensagem por IlgssonBraga

Qui Jul 18, 2013 13:36
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


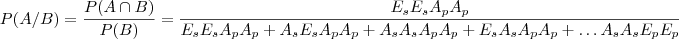 aqui vc terá que analisar todas as 16 combinações possíveis. como as chances de acerto e erro são iguais cada uma delas é de
aqui vc terá que analisar todas as 16 combinações possíveis. como as chances de acerto e erro são iguais cada uma delas é de 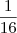 . assim
. assim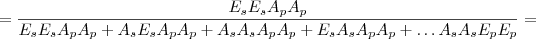

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.