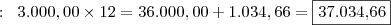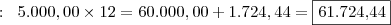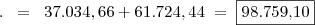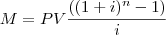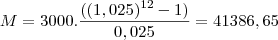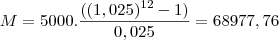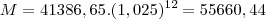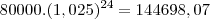[O valor de um equipamento é de R$ 80.000,00. Como alternativa, o fornecedor aluga o equipamento por dois anos, sendo de R$ 3.000,00 o aluguer mensal no primeiro ano e de R$ 5.000,00 o aluguer mensal no segundo ano, vencendo o aluguer ao final de cada mês. O equipamento, no final do contrato, é vendido ao cliente pelo seu valor residual. Qual é esse valor residual, se a taxa de juros da operação for de 2,5% a.m. ?]
Olá pessoal do "ajudamatemática". Como vêem sou novo por aqui.
Não sei ao certo, se quando referem __ " Favor especificar correctamente o tema do seu tópico entre [...] conforme formato exemplo acima"__ se estão a referir que é o enunciado do problema a colocar, que deve ficar entre parêntesis rectos tal como eu fiz. Mas como em ___ "Formato obrigatório"___ diz:___ [tema principal primeiro] seu assunto livre depois___ eu deduzo que seja assim.__Tema principal__ o enunciado do problema colocado entre [...]__ seu assunto livre depois ___ as dúvidas que tivermos a colocar relativamente ao dito problema fora dos parêntesis. Se assim não for, peço desculpa pelo mal entendido, e se possível corrijam este meu erro de postagem, e me esclareçam para evitar erros futuros.
P.S.____ Creio que seja desta forma que pretendam que se coloque o Título.___ [Matemática Financeira] Valor residual. Tal como postei agora.
Mas vamos ao problema.
Dados:
__ Valor comercial do equipamento, novo, ou já usado e numa determinada altura da sua existência = R$ 80.000,00
__ Como alternativa,(creio que a uma possível venda, ou para não estar inactivo a degradar-se) é alugado por 2 anos:
__ 1º Ano R$ 3.000,00 x 12 = R$ 36.000,00
__ 2º Ano R$ 5.000,00 x 12 = R$ 60.000,00
__ É vendido ao cliente no final do contracto,(i.e.,passados os 2anos) pelo seu valor residual (valor ao fim do qual, o equipamento está completamente desgastado, e é considerado como sucata.) Assim o creio.
__ Qual o seu Valor Residual se a taxa de juros da operação for de 2,5% ao mês.
Solução: R$ 20.059,85
Minhas dúvidas:
__ Sobre que valores se aplica a taxa de juros mensal da operação ? __ Creio que seja sobre os valores das prestações mensais. 3.000 x 0,025 a.m. = 75
5.000 x 0,025 a.m. = 125
__ 1ª Prestação mensal com os respectivos juros relativamente ao 1º ano ------> 3.000 + 75 = 3.075
__ 2ª Prestação mensal com os respectivos juros relativamente ao 2º ano ------> 5.000 + 125 = 5.125
__ Total das prestações + juros relativos ao aluguer do equipamento durante o 1 º ano ------> 3.075 x 12 = 36.900
__ Total de prestações + juros relativos ao aluguer do equipamento durante o 2º ano --------> 5.125 x 12 = 61.500
__ Total da despesa com o aluguer do equipamento durante os 2 anos -------> 36.900 + 61.500 = 98.400
__ Estive pesquisando na Net e conclui, não sei se correctamente que :__ O Valor residual = Valor de Custo - Depreciação acumulada ao fim de n anos.
Perante isto, não sei mais como proceder.
Pergunto, se o que fiz até aqui está certo,e é essencial para a resolução do problema, e em caso afirmativo, o que falta ainda fazer para chegar à solução.
Antecipadamente grato
Armando



![:J=PV.[(1+i )^n-1]\;\;\Longrightarrow \;\;J=3.000.[(1+0,025)^{12}-1]\;\;\Longrightarrow\;\;J = 1.034,66 :J=PV.[(1+i )^n-1]\;\;\Longrightarrow \;\;J=3.000.[(1+0,025)^{12}-1]\;\;\Longrightarrow\;\;J = 1.034,66](/latexrender/pictures/d45ecf8e806a35b67efe711aadb44019.png)
![:J=PV.[(1+i)^n-1]\;\;\Longrightarrow \;\;J=5.000.[(1+0,025)^{12}-1]\;\;\Longrightarrow\;\;J = 1.724,44 :J=PV.[(1+i)^n-1]\;\;\Longrightarrow \;\;J=5.000.[(1+0,025)^{12}-1]\;\;\Longrightarrow\;\;J = 1.724,44](/latexrender/pictures/c39ede83bbab80b1c34e0d6d6c6bca77.png)