 por Victor Franca » Seg Mar 04, 2013 21:05
por Victor Franca » Seg Mar 04, 2013 21:05
Provar por PIF:
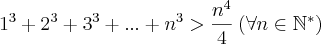
Como faria?
Fiz assim, primeiro:
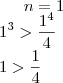
Segundo:
(Hipótese)
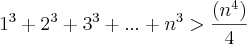
Provando:
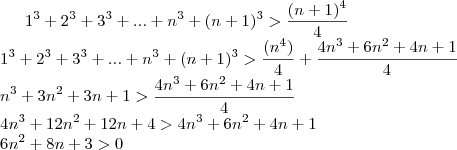
Para qualquer número natural não nulo essa proposição é verdadeira.
Seria assim? Me parece que ficou meio vago provar dessa forma, apesar de realmente a última proposição ser verdadeira.
Outra questão é a seguinte:
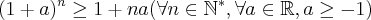
Essa eu estou me embolando... Não estou conseguindo iniciar a questão
O ruim dos livros do Iezzi é que o gabarito é muito incompleto...
-
Victor Franca
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mar 04, 2013 20:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Seg Mar 04, 2013 23:43
por young_jedi » Seg Mar 04, 2013 23:43
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Princípio da Indução Finita
por Fontelles » Dom Jan 17, 2010 14:42
- 9 Respostas
- 105796 Exibições
- Última mensagem por Vennom

Qui Abr 26, 2012 23:04
Funções
-
- PIF - Principio da Indução Finita
por ederj » Seg Jun 28, 2010 13:35
- 3 Respostas
- 8065 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 20:01
Funções
-
- Princípio de Indução Finita (PIF)
por Jorge Rodrigo » Qui Jun 09, 2011 17:37
- 1 Respostas
- 5448 Exibições
- Última mensagem por MarceloFantini

Qui Jun 09, 2011 20:44
Álgebra Elementar
-
- Princípio da Indução Finita
por silvia fillet » Qui Out 20, 2011 12:04
- 3 Respostas
- 9417 Exibições
- Última mensagem por silvia fillet

Sex Out 21, 2011 17:33
Álgebra Elementar
-
- [PIF] Princípio de indução finita
por Beckyh » Qua Abr 11, 2012 06:45
- 2 Respostas
- 6396 Exibições
- Última mensagem por Beckyh

Qui Abr 12, 2012 00:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
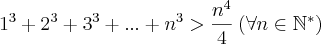
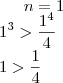
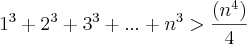
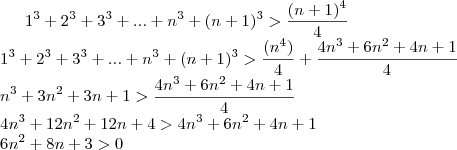
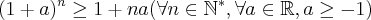


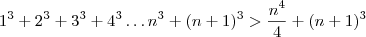
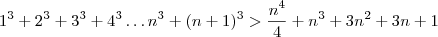
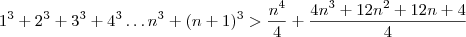
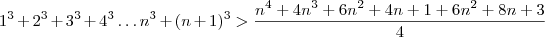
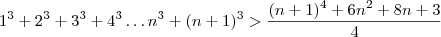
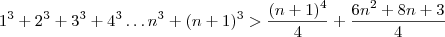
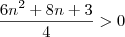
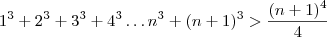


 .
.
 :
: