 por PedroCunha » Qui Nov 15, 2012 08:36
por PedroCunha » Qui Nov 15, 2012 08:36
Olá. Achei esta questão na internet
(ITA – SP) – A equação
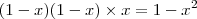
tem:
a. Três raízes reais;
b. Uma raiz dupla igual a 1;
c. Não tem raízes complexas;
d. S = {1; i ; - i};
e. Nda.
e não estou conseguindo fazer ela.
Tentei usar produtos notáveis para reduzir a equação, mas cheguei em uma equação de segundo grau, o que está errado, pois a resposta certa é a letra
D Alguém poderia me mostrar como fazer?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Nov 15, 2012 13:54
por DanielFerreira » Qui Nov 15, 2012 13:54
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Sex Nov 16, 2012 19:04
por PedroCunha » Sex Nov 16, 2012 19:04
Olá. Primeiramente, obrigado por responder. Porém, tenho uma dúvida.
Quando você chega em:
![( 1 - x ) ( 1 - x )x - ( 1 + x ) ( 1 - x) = 0
( 1 - x ) [x( 1 - x ) - ( 1 + x)] = 0 ( 1 - x ) ( 1 - x )x - ( 1 + x ) ( 1 - x) = 0
( 1 - x ) [x( 1 - x ) - ( 1 + x)] = 0](/latexrender/pictures/196f2c8dff9b7c4f47340c1111458a5a.png)
O que acontece com o segundo

do produto
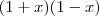
Att.,
Pedro
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 17, 2012 17:07
por DanielFerreira » Sáb Nov 17, 2012 17:07
Olá Pedro,
boa tarde!
Eu coloquei ele em evidência, isto é, dividi!
(1 - x)(1 - x)x - (1 + x)(1 - x) = 0
(1 - x)[(1 - x)x - (1 + x)] = 0
Consegue visualizar?
Aguardo retorno.
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Sáb Nov 17, 2012 17:50
por PedroCunha » Sáb Nov 17, 2012 17:50
Mas nesse caso, devido à presença do

isso não estaria errado?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 17, 2012 18:02
por DanielFerreira » Sáb Nov 17, 2012 18:02
Veja um exemplo:
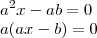
Note que,
1 - x = a
1 + x = b
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Sáb Nov 17, 2012 18:45
por PedroCunha » Sáb Nov 17, 2012 18:45
Ahhh..acho que agora entendi.Veja se meu raciocínio está correto. Na equação
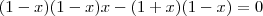
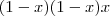
são como se fosse um só
e
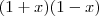
também são como se fosse um só
Por isso, quando colocamos o

em evidência, chegamos em
![(1-x) [ (1-x)x - (1+x)] (1-x) [ (1-x)x - (1+x)]](/latexrender/pictures/f2d2e916eada749ad14ab7f7b614b6bf.png)
Certo?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 17, 2012 18:46
por DanielFerreira » Sáb Nov 17, 2012 18:46
Perfeito!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Sáb Nov 17, 2012 18:49
por PedroCunha » Sáb Nov 17, 2012 18:49
Obrigado pela atenção!
Não estava entendendo pois estava olhando os termos como se fossem separados. Logo, não conseguia entender. Mas só por curiosidade, se eu não soubesse isso, teria como resolver o exercício sem colocar nada em evidência?
Att.,
Pedro
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por PedroCunha » Sáb Nov 17, 2012 18:51
por PedroCunha » Sáb Nov 17, 2012 18:51
Obrigado pela atenção!
Não estava entendendo pois estava olhando os termos como se fossem separados. Logo, não conseguia entender. Mas só por curiosidade, se eu não soubesse isso, teria como resolver o exercício sem colocar nada em evidência?
Att.,
Pedro
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 17, 2012 19:17
por DanielFerreira » Sáb Nov 17, 2012 19:17
Queres outra forma de resolver, certo?!
Segue:

Agora, teria que encontrar as raízes dessa equação do 3º grau.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Sáb Nov 17, 2012 19:38
por PedroCunha » Sáb Nov 17, 2012 19:38
Para encontrar as raízes dessa equação teria que colocar em evidência também, certo?
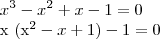
1ª equação:
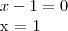
2ª equação:
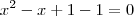


O resultado está errado. Eu que fiz errado ou esse é o jeito errado de resolver?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Nov 18, 2012 10:22
por DanielFerreira » Dom Nov 18, 2012 10:22
PedroCunha escreveu:Para encontrar as raízes dessa equação teria que colocar em evidência também, certo?
Acredito que essa seja a forma mais simples.
Dê uma olhada nesse tópico
http://www.ajudamatematica.com/viewtopic.php?f=116&t=10230&p=35729#p35729.
Mas, existe outra forma...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Dom Nov 18, 2012 10:53
por PedroCunha » Dom Nov 18, 2012 10:53
Ahh..entendi o jeito de certo de fatorar. Aqui vai conta, veja se está certa por favor.
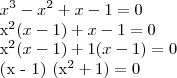
1ª Resposta:

2ª Resposta:
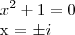
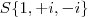
Att.,
Pedro
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Ter Nov 20, 2012 21:07
por DanielFerreira » Ter Nov 20, 2012 21:07
Sim, está certo!

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PedroCunha » Ter Nov 20, 2012 21:31
por PedroCunha » Ter Nov 20, 2012 21:31
Obrigado por toda a ajuda Dan,

.
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas sobre polinômios
por Lorraine » Sex Mai 13, 2011 10:17
- 1 Respostas
- 2064 Exibições
- Última mensagem por FilipeCaceres

Sex Mai 13, 2011 11:22
Polinômios
-
- [polinômios] questão uel
por Flavia R » Ter Ago 30, 2011 12:45
- 0 Respostas
- 1816 Exibições
- Última mensagem por Flavia R

Ter Ago 30, 2011 12:45
Polinômios
-
- Polinômios - Questão
por iceman » Dom Mai 27, 2012 18:23
- 1 Respostas
- 1556 Exibições
- Última mensagem por DanielFerreira

Dom Mai 27, 2012 18:26
Polinômios
-
- Polinômios - Questão
por iceman » Dom Mai 27, 2012 23:51
- 1 Respostas
- 1492 Exibições
- Última mensagem por Cleyson007

Ter Mai 29, 2012 17:39
Polinômios
-
- Questão de Intervalo em Polinômios
por joedsonazevedo » Qui Nov 15, 2012 11:34
- 1 Respostas
- 1768 Exibições
- Última mensagem por DanielFerreira

Qui Nov 15, 2012 13:31
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
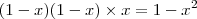 tem:
tem:

![\\ (1 - x)(1 - x)x = 1 - x^2 \\\\ (1 - x)(1 - x)x = (1 + x)(1 - x) \\\\ (1 - x)(1 - x)x - (1 + x)(1 - x) = 0 \\\\ (1 - x)\left [ x(1 - x) - (1 + x) \right ] = 0 \\\\ (1 - x)(\cancel{x} - x^2 - 1 \cancel{- x}) = 0 \\\\ (1 - x)(- x^2 - 1) = 0 \\\\ (1 - x) \cdot - 1 \cdot (x^2 + 1) = 0 \\\\ - (1 - x)(x^2 + 1) = 0 \\\\ (x - 1)(x^2 + 1) = 0 \\\\ \begin{cases} x - 1 = 0 \\ x^2 + 1 = 0 \end{cases} \\\\\\ \blacklozenge \,\, x - 1 = 0 \\ \boxed{\boxed{x = 1}} \\\\\\ \blacklozenge \,\, x^2 + 1 = 0 \\ \Delta = 0 - 4 \\ \Delta = - 4 \\ \Delta = 4i^2 \\\\ x = \frac{0 \pm \sqrt{4i^2}}{2} \\\\ \boxed{\boxed{x' = i}} \,\, \textup{e} \,\, \boxed{\boxed{x' = - i}} \\ (1 - x)(1 - x)x = 1 - x^2 \\\\ (1 - x)(1 - x)x = (1 + x)(1 - x) \\\\ (1 - x)(1 - x)x - (1 + x)(1 - x) = 0 \\\\ (1 - x)\left [ x(1 - x) - (1 + x) \right ] = 0 \\\\ (1 - x)(\cancel{x} - x^2 - 1 \cancel{- x}) = 0 \\\\ (1 - x)(- x^2 - 1) = 0 \\\\ (1 - x) \cdot - 1 \cdot (x^2 + 1) = 0 \\\\ - (1 - x)(x^2 + 1) = 0 \\\\ (x - 1)(x^2 + 1) = 0 \\\\ \begin{cases} x - 1 = 0 \\ x^2 + 1 = 0 \end{cases} \\\\\\ \blacklozenge \,\, x - 1 = 0 \\ \boxed{\boxed{x = 1}} \\\\\\ \blacklozenge \,\, x^2 + 1 = 0 \\ \Delta = 0 - 4 \\ \Delta = - 4 \\ \Delta = 4i^2 \\\\ x = \frac{0 \pm \sqrt{4i^2}}{2} \\\\ \boxed{\boxed{x' = i}} \,\, \textup{e} \,\, \boxed{\boxed{x' = - i}}](/latexrender/pictures/71765d5b44e0ba5d06b9cf3b56a72b74.png)

![( 1 - x ) ( 1 - x )x - ( 1 + x ) ( 1 - x) = 0
( 1 - x ) [x( 1 - x ) - ( 1 + x)] = 0 ( 1 - x ) ( 1 - x )x - ( 1 + x ) ( 1 - x) = 0
( 1 - x ) [x( 1 - x ) - ( 1 + x)] = 0](/latexrender/pictures/196f2c8dff9b7c4f47340c1111458a5a.png)

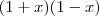
 isso não estaria errado?
isso não estaria errado?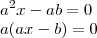
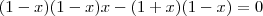
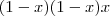 são como se fosse um só
são como se fosse um só 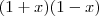 também são como se fosse um só
também são como se fosse um só em evidência, chegamos em
em evidência, chegamos em![(1-x) [ (1-x)x - (1+x)] (1-x) [ (1-x)x - (1+x)]](/latexrender/pictures/f2d2e916eada749ad14ab7f7b614b6bf.png)

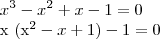
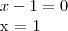
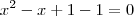


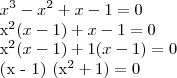

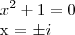
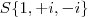

 .
.