sou novo no Forum e estou com uma dúvida de Matemática Financeira (que nunca estudei, embora tenha interesse).
Eu desejo investir V reais, todo mês, a uma taxa mensal de juros compostos i por t meses, e queria saber se é possível calcular o valor total futuro desse investimento.
Eu sei que, após os primeiros meses, eu tería o seguinte:
Ao final do mês 1 (t=1) =
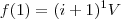
Mês 2 (t=2) =
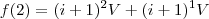
Mês 3 (t=3) =
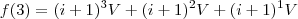
Então, me parece que teríamos a seguinte fórmula geral:
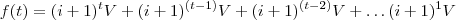
Ou, unindo os termos:
![f(x)=V[(i+1)^t+(i+1)^{(t-1)}+(i+1)^{(t-2)}+\ldots\+(i+1)^1]](/latexrender/pictures/7ca1de126c85471cf7f6d4c5256b467f.png "f(x)=V[(i+1)^t+(i+1)^{(t-1)}+(i+1)^{(t-2)}+\ldots\+(i+1)^1]")
Gostaria de saber se isso está correto! Se sim, qual é a melhor maneira de se calcular a soma?? Porque eu vejo colegas fazendo cálculos para 600 meses, a taxas compostas de, por exemplo, 1,01% ao mes, sobre R$300 que são adicionados mensalmente, e penso que deve haver uma forma mais fácil do que sair somando e multiplicando todos esses termos na calculadora.
Desde já, muitíssimo grato!
João
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.