 por natanskt » Sex Out 15, 2010 19:18
por natanskt » Sex Out 15, 2010 19:18
2)(EEAR)SEJA A FUNÇÃO
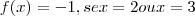
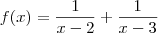
se x diferente de 2,e x diferente de 3
o valor da razão

é:
a-)-3/2
d-)-1/2
c-)1/2
d-)3/2
galera,o f(x) eu coloquei duas vezes,mais na questão aqui ta um só,e tem uma chave encobrindo as duas conta f(x)={
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Neperiano » Sex Out 15, 2010 20:29
por Neperiano » Sex Out 15, 2010 20:29
Ola
Não sei qual a sua duvida mas,
Primeiro calcule f(1) através da segunda equação depois calcule f(3) com a segunda equação
Como voce sabe que f(3) = 1
A razão vai ser algum numero divido por 1, então calcule f(1) que deve dar -1/2
Qualquer duvida atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Sex Out 15, 2010 20:37
por MarceloFantini » Sex Out 15, 2010 20:37
Natanskt, basta calcular
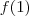
e dividir por
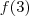
. Onde está a sua dificuldade?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por natanskt » Sex Out 15, 2010 23:15
por natanskt » Sex Out 15, 2010 23:15
fantini me ajuda aew
bom eu tenho que fazer isso?
f(3) eu coloco -1
e onde tem
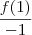
assim?
o o f(1) eu não sei
por favor...e que eu comprei umas apostilas é só vem com 3exemplo,eu não consigo aprender
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Elcioschin » Sáb Out 16, 2010 19:13
por Elcioschin » Sáb Out 16, 2010 19:13
f(x) = 1/(x - 2) + 1/(x - 3) ----> Para x = 1 ----> f(1) = 1/(1 - 2) + 1/(1 - 3) ----> f(1) = - 1 - 1/2 ----> f(1) = - 3/2
f(1)/f(3) = (-3/2)/-1 -----> f(1)/f(3) = 3/2 ----> Alternativa D
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (EEAR)Função
 por natanskt » Sex Out 15, 2010 19:08
por natanskt » Sex Out 15, 2010 19:08
- 6 Respostas
- 6619 Exibições
- Última mensagem por DanielRJ

Sáb Out 16, 2010 16:57
Funções
-
- (EEAR)Função
por natanskt » Ter Out 19, 2010 10:40
- 1 Respostas
- 2475 Exibições
- Última mensagem por DanielRJ

Ter Out 19, 2010 16:37
Funções
-
- (EEAR)Função
por natanskt » Qua Out 20, 2010 12:04
- 1 Respostas
- 2129 Exibições
- Última mensagem por DanielRJ

Qua Out 20, 2010 12:25
Funções
-
- (EEAR)Função 2 grau
por natanskt » Sex Out 22, 2010 11:54
- 3 Respostas
- 2016 Exibições
- Última mensagem por DanielFerreira

Sex Nov 19, 2010 19:14
Funções
-
- (EEAR)Função 2 grau
por natanskt » Sex Out 22, 2010 13:57
- 1 Respostas
- 1108 Exibições
- Última mensagem por MarceloFantini

Sex Out 22, 2010 14:34
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
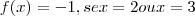
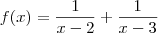 se x diferente de 2,e x diferente de 3
se x diferente de 2,e x diferente de 3 é:
é:
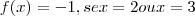
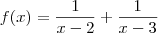 se x diferente de 2,e x diferente de 3
se x diferente de 2,e x diferente de 3 é:
é:

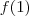 e dividir por
e dividir por 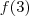 . Onde está a sua dificuldade?
. Onde está a sua dificuldade?

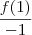 assim?
assim?

