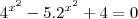
a-)2
b-)5
c-)
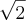
d-)1
e-)

minha tentativa de resolução...!
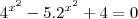
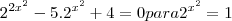
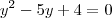 só que da errado
só que da erradoa alternativa correta do gabarito é C
ajuda galera
por favor!!!

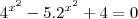
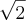

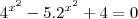
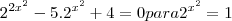
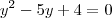 só que da errado
só que da errado
 sendo que o y agora você já sabe porque você acho quando resolveu a equação do 2°Grau , ou você se enganou com as váriaveis resolvendo para y ao invez de para x. Sugiro que reveja as contas mas se mesmo assim não estiver batendo leia a resolução.
sendo que o y agora você já sabe porque você acho quando resolveu a equação do 2°Grau , ou você se enganou com as váriaveis resolvendo para y ao invez de para x. Sugiro que reveja as contas mas se mesmo assim não estiver batendo leia a resolução.
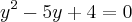 Resolvendo essa equação por soma e produto, temos:
Resolvendo essa equação por soma e produto, temos: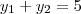 e
e 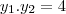 Sendo
Sendo  e
e 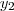 As raizes da equação do segundo grau,resolvendo esse sistema ,temos:
As raizes da equação do segundo grau,resolvendo esse sistema ,temos: e
e 
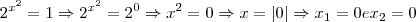
![{2}^{{x}^{2}} = 4\Rightarrow {2}^{{x}^{2}}={2}^{2}\Rightarrow {x}^{2}=2\Rightarrow x = \left| \sqrt[2]{2}\right|\Rightarrow {x}_{3}= \sqrt[2]{2} e{x}_{4}=-\sqrt[2]{2} {2}^{{x}^{2}} = 4\Rightarrow {2}^{{x}^{2}}={2}^{2}\Rightarrow {x}^{2}=2\Rightarrow x = \left| \sqrt[2]{2}\right|\Rightarrow {x}_{3}= \sqrt[2]{2} e{x}_{4}=-\sqrt[2]{2}](/latexrender/pictures/6724ce4951832ac0896abcba333abfbe.png)
![S = \sqrt[2]{2} S = \sqrt[2]{2}](/latexrender/pictures/58b75140850569f9d624a5d3d912be67.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante