 por DanielRJ » Seg Set 20, 2010 17:51
por DanielRJ » Seg Set 20, 2010 17:51
Olá to com uma questão muito dificil pra min então gostaria que alguem em ajudasse.
Em uma prova caíram dois problemas, A e B. Sabendo que 200 alunos acertaram A, 90 erraram B, 120 acertaram os dois e 100 acertaram apenas um problema, qual a probabilidade de que um aluno, escolhido ao acaso, não tenha acertado nenhum problema.
a)1/23
b)2/23
c)3/23
d)1/8
e)1/12
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Seg Set 20, 2010 20:29
por alexandre32100 » Seg Set 20, 2010 20:29
É aconselhável nestes casos usar um
Diagrama de Venn, onde cada número representa aqueles que acertaram determinada questão, veja:
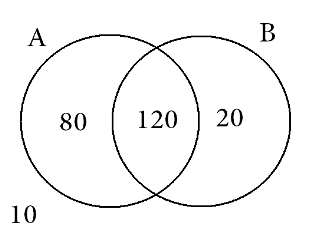
- é semprebom lembrar de sempre começar pelo "meio" do diagrama
- DIAGRAMA.PNG (10.37 KiB) Exibido 6859 vezes
O número total de alunos é
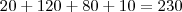
e aqueles que não acertaram nenhuma questão,

.
Assim, a probabilidade é
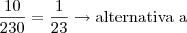
.
-
alexandre32100
-
 por DanielRJ » Seg Set 20, 2010 22:00
por DanielRJ » Seg Set 20, 2010 22:00
alexandre32100 escreveu:É aconselhável nestes casos usar um
Diagrama de Venn, onde cada número representa aqueles que acertaram determinada questão, veja:
DIAGRAMA.PNG
O número total de alunos é
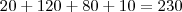
e aqueles que não acertaram nenhuma questão,

.
Assim, a probabilidade é
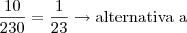
.
Obrigado alexandre. mas minha dificuldade foi em montar os conjuntos. eu queria que voce me desse uma explicação rapida de onde sairam os 20 de B e os 10 de fora?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Ter Set 21, 2010 00:11
por alexandre32100 » Ter Set 21, 2010 00:11
Tá, a parte dos

da interseção de

e

e dos
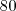
de

tá ok, né?
Os
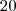
de

tão aqui, olha
danielcdd escreveu:100 acertaram apenas um problema
Como
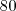
acertaram
apenas 
, quer dizer que
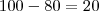
acertaram apenas

.
E os

de fora, aqui
danielcdd escreveu:90 erraram B
já que
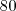
acertaram apenas

, precisamos de mais

para completar esses
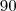
(já que os outros
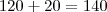
acertaram o problema

).
Tranquilo agora?
-
alexandre32100
-
 por DanielRJ » Ter Set 21, 2010 12:53
por DanielRJ » Ter Set 21, 2010 12:53
alexandre32100 escreveu:Tá, a parte dos

da interseção de

e

e dos
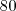
de

tá ok, né?
Os
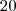
de

tão aqui, olha
danielcdd escreveu:100 acertaram apenas um problema
Como
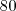
acertaram
apenas 
, quer dizer que
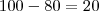
acertaram apenas

.
E os

de fora, aqui
danielcdd escreveu:90 erraram B
já que
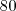
acertaram apenas

, precisamos de mais

para completar esses
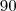
(já que os outros
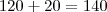
acertaram o problema

).
Tranquilo agora?
Bom muito obrigado realmente minha dificuldade é conjuntos vo estudar mais afundo essa materia, Mas eu compreendi o entendimento da questão muito obrigado mais uma duvida liquidada.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10349 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21660 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5349 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4525 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4536 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


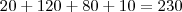 e aqueles que não acertaram nenhuma questão,
e aqueles que não acertaram nenhuma questão,  .
.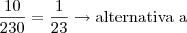 .
. da interseção de
da interseção de  e
e  e dos
e dos 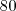 de
de 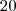 de
de 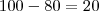 acertaram apenas
acertaram apenas 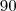 (já que os outros
(já que os outros 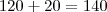 acertaram o problema
acertaram o problema 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.