Olá venho postar uma questão que estou com duvidas.
Jogando-se um dado duas vezes, qual a probabilidade de obter a soma dos pontos um numero menor que 6?
a)5/18
b)1/3
c)7/18
d)11/36
Possiveis:
1+1 2+1 3+1 4+1
1+2 2+2 3+2
1+3 2+3
1+4
para cada é 1/36.
bom galera a questão é simples, mas o probleema é eu terei que esboçar todas as possibilidades possiveis ou há algum jeito para eu ganhar tempo?


 , onde
, onde 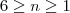 . Para o outro dado, há
. Para o outro dado, há  possibilidades para que seja menor que
possibilidades para que seja menor que  . Assim, o resultado que procuramos é
. Assim, o resultado que procuramos é 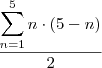 (dividimos a soma por dois porque cada caso foi contado duas vezes, a ordem dos dados não é levada em conta, diferentemente do que propus inicialmente), o que é o mesmo que
(dividimos a soma por dois porque cada caso foi contado duas vezes, a ordem dos dados não é levada em conta, diferentemente do que propus inicialmente), o que é o mesmo que 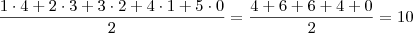 . Por fim, a probabilidade é
. Por fim, a probabilidade é 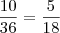 .
.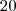 faces em que queremos uma soma menor que
faces em que queremos uma soma menor que 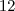 .
.
 .
.
 :
: