Caros colegas , mais um pepino...(pelo menos pra mim,rs)
Tenho uma amostra dividida em dez classes (nº de vitmas por Km em uma rodovia). O exercicio pede a probabilidade de se ter 3 pessoas acidentadas entre os quilometros 0 e 25 (primeiro intervalo da classe) e de 10 pessoas acidentadas entre os quilometros 50 e 75
No trecho 0 - 25, o numero total de vítimas foi 238.
No trecho 50 - 75 o numero total de vitimas foi 25
O total geral de nº de vitimas foi de 352, ou seja 68% foi dentro no trecho (0 - 25) e 6% no trecho (50 - 750
Como faço para calcular estas probabilidades? Devo levar em consideração o numero total de vitimas da amostra ou apenas trabalhar dentro de cada intervalo?
Por favor, ajudem-me!
Desde já agradecida
Márcia



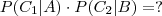
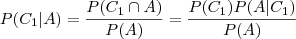
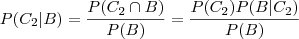
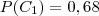
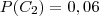
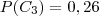
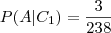
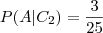
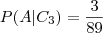
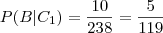
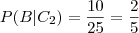
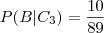
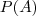 e
e 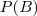 (denominador), pois o numerador é conhecido.
(denominador), pois o numerador é conhecido. por ser reescrito assim:
por ser reescrito assim:

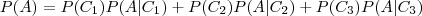
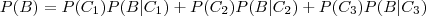
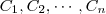 é uma partição do espação amostral
é uma partição do espação amostral 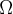 , ou seja,
, ou seja, 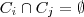 , sempre que
, sempre que 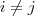 . E
. E 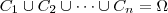 .
.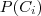 e
e 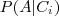 ,
, 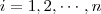 , a probabilidade de ocorrênia do evento
, a probabilidade de ocorrênia do evento  , supondo-se a ocorrência do evento
, supondo-se a ocorrência do evento 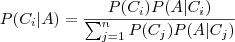
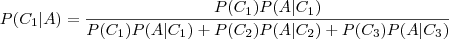
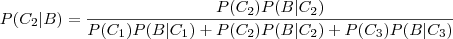
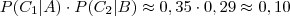 .
.
 .
.



