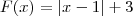 , analise as afirmativas seguintes:
, analise as afirmativas seguintes:1- Umao utra forma de expressar a lei define
 é
é 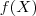 =
= 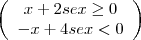
2- o conjunto imagem de
 é o intervalo [3, + ?[
é o intervalo [3, + ?[3-
 é crescente no intervalo ]- ?,1[
é crescente no intervalo ]- ?,1[4- se
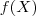
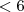 entao -2 < x < 4
entao -2 < x < 45- o gráfico de
 intercepta o eixo das abscissas no ponto
intercepta o eixo das abscissas no ponto 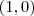
Gabarito: f v f v f
To muito fraco de modular, fazia tempo que nao via . so to sabendo akele básico quando a equação todo esta no modula, alguem pode me ajudar nessa questão?




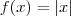
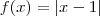
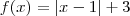
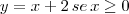

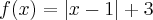
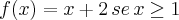
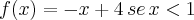
 1" ou "X<1". Espero ter podido auxiliá-los, ok? Muito agradecido a todos e é muito bom saber que agora poderei recorrer aos meus novos colegas, pois assim saberei que não sou um solitário amante da matemática! Tudo de bom e até mais...
1" ou "X<1". Espero ter podido auxiliá-los, ok? Muito agradecido a todos e é muito bom saber que agora poderei recorrer aos meus novos colegas, pois assim saberei que não sou um solitário amante da matemática! Tudo de bom e até mais...