 por adauto martins » Qua Set 25, 2019 21:43
por adauto martins » Qua Set 25, 2019 21:43
(este-ita,escola tecnica do exercito,instituto tecnologico de aeronautica-exame de admissao 1947)
calcular o cosseno da soma dos angulos que satisfazem as equaçoes dos sistema abaixo:
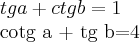
ps-o curso de engenharia aeronautica foi criado em 1939 e ministrado na escola tecnica(Es.T.E(1933/58) do exercito ate 1949.
a partir de 1947,o exame para as turmas que formaria na nova escola,ITA(instituto tecnologico de aeronautica)edificada de 1948/1950 em sao jose dos campos, eram ainda prestada nos exames da escola tecnica do exercito(Es.T.E)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Set 26, 2019 10:56
por adauto martins » Qui Set 26, 2019 10:56
soluçao:
as raizes complexas da unidade
![\sqrt[5]{1} \sqrt[5]{1}](/latexrender/pictures/76f12af45d6e844ebf09ab99f00cc9f1.png)
,serao dadas por:
![\sqrt[5]{1}=\sqrt[5]{\left|1 \right|}(cos(2k\pi/)+se(2k\pi/5)i \sqrt[5]{1}=\sqrt[5]{\left|1 \right|}(cos(2k\pi/)+se(2k\pi/5)i](/latexrender/pictures/ae14277c766b116e93fd0e6f456b2462.png)
sabendo que
![\sqrt[5]{\left|1 \right|}=1,\theta=0 \sqrt[5]{\left|1 \right|}=1,\theta=0](/latexrender/pictures/378e8072dbd6d7096e419baccb2fd64b.png)
e
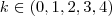
,entao:
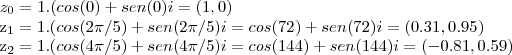
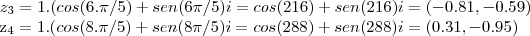
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Set 30, 2019 19:26
por adauto martins » Seg Set 30, 2019 19:26
soluçao :
de (1),temos:
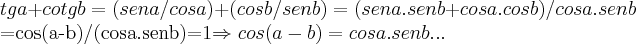
de(2)...
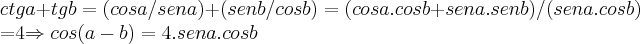
,logo:
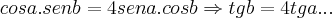
substituindo em (1),teremos:
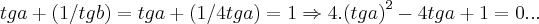
aqui e resolver essa equaçao do segundo grau,achar o valor de a,e consequentemente o valor de b,
com as devidas restriçoes de angulos da tangente(tangentes) e encontrar o pedido de cos(a+b)=...termine-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:41
- 1 Respostas
- 12343 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:53
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:51
- 1 Respostas
- 12639 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:45
Polinômios
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:02
- 1 Respostas
- 4923 Exibições
- Última mensagem por adauto martins

Qui Set 19, 2019 09:39
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:09
- 4 Respostas
- 8711 Exibições
- Última mensagem por adauto martins

Sex Out 11, 2019 10:34
Números Complexos
-
- exerc.proposto
por adauto martins » Ter Set 17, 2019 10:30
- 1 Respostas
- 4222 Exibições
- Última mensagem por adauto martins

Seg Set 23, 2019 23:57
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
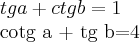


![\sqrt[5]{1} \sqrt[5]{1}](/latexrender/pictures/76f12af45d6e844ebf09ab99f00cc9f1.png) ,serao dadas por:
,serao dadas por:![\sqrt[5]{1}=\sqrt[5]{\left|1 \right|}(cos(2k\pi/)+se(2k\pi/5)i \sqrt[5]{1}=\sqrt[5]{\left|1 \right|}(cos(2k\pi/)+se(2k\pi/5)i](/latexrender/pictures/ae14277c766b116e93fd0e6f456b2462.png)
![\sqrt[5]{\left|1 \right|}=1,\theta=0 \sqrt[5]{\left|1 \right|}=1,\theta=0](/latexrender/pictures/378e8072dbd6d7096e419baccb2fd64b.png) e
e 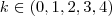 ,entao:
,entao: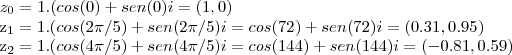
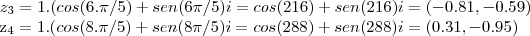
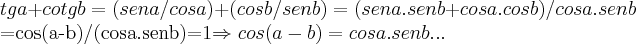
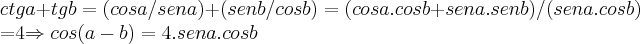 ,logo:
,logo: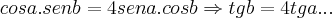
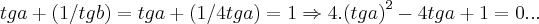
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.