Problema:
"De um campeonato de futebol participaram 12 times, 2 gaúchos, 2 mineiros, 4 paulistas e 4 cariocas. De quantos modos pode ser formado o grupo dos quatro primeiros colocados se o primeiros lugar deve ser ocupado sempre por um time gaúcho?"
Amigos, alguém sugere uma solução segura para este problema? Estou com dificuldade de organizar as repetições na contagem.
Obrigado.


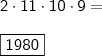


 .
.



