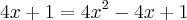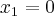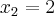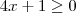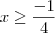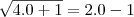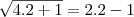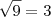por luanxd » Dom Fev 28, 2010 03:05
por luanxd » Dom Fev 28, 2010 03:05
O conjunto de soluções Inteiras da equação
![\sqrt[]{4x+1}=2x-1 \sqrt[]{4x+1}=2x-1](/latexrender/pictures/c1907162de14a3f4867b63b93d1a2aff.png)
:
a){2}
b{0,2}
c){o,1/2}
d){0}
e){1/2}
Obrigado pela atenção!
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Dom Fev 28, 2010 09:04
por Cleyson007 » Dom Fev 28, 2010 09:04
Bom dia luanxd!
Segue resolução:
![\sqrt[2]{4x+1}=2x-1 \sqrt[2]{4x+1}=2x-1](/latexrender/pictures/a7605258dc6e58bb6600cbb4da550262.png)
Elevando os dois lados ao quadrado (para sumir com a raiz), temos:
^{2}=(2x-1)^2 {\sqrt[2]({4x+1}})^{2}=(2x-1)^2](/latexrender/pictures/3faee9cde73dd15d7348783fd93c1e09.png)
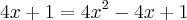
Resolvendo a equação do segundo grau:
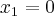
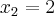
Alternativa
b está correta!
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Dom Fev 28, 2010 15:14
por MarceloFantini » Dom Fev 28, 2010 15:14
Boa tarde.
Cleyson, lembre-se da condição de existência:
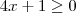
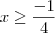
Neste caso as duas raízes satisfazem, porém é preciso testá-las pra verem se as duas são soluções:
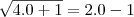

Absurdo. 0 não é raíz da equação. Vamos testar o 2:
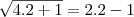
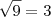
Satisfaz a equação. Portanto, só 2 é raíz.
Resposta letra A.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Dom Fev 28, 2010 16:13
por Cleyson007 » Dom Fev 28, 2010 16:13
Boa tarde Fantini!
Realmente.. acabou passando despercebido..
Seria um absurdo se o 0 fosse raiz da equação, encontraria:
1 = -1
Obrigado por comentar

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por luanxd » Dom Fev 28, 2010 17:32
por luanxd » Dom Fev 28, 2010 17:32
Obrigado pela ajuda!
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{4x+1}=2x-1 \sqrt[]{4x+1}=2x-1](/latexrender/pictures/c1907162de14a3f4867b63b93d1a2aff.png) :
:
![\sqrt[2]{4x+1}=2x-1 \sqrt[2]{4x+1}=2x-1](/latexrender/pictures/a7605258dc6e58bb6600cbb4da550262.png)
^{2}=(2x-1)^2 {\sqrt[2]({4x+1}})^{2}=(2x-1)^2](/latexrender/pictures/3faee9cde73dd15d7348783fd93c1e09.png)