 por Pessoa Estranha » Qui Nov 28, 2013 16:08
por Pessoa Estranha » Qui Nov 28, 2013 16:08
Olá .... Gostaria de uma sugestão para resolver questões do seguinte tipo:
"Suponha

contínua em [-1,1]. Calcule
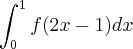
sabendo que
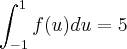
."
Sei que, nestes casos, é interessante usar o Teorema da Mudança de Variável. Por outro lado, não estou sabendo o que fazer com a própria função. É claro que isto só mostra que eu não entendi o verdadeiro valor do Teorema citado e soube aplicá-lo apenas nos casos mais gerais. Por gentileza, ajudem-me; preciso apenas de uma sugestão. Obrigada !
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Qui Nov 28, 2013 18:38
por young_jedi » Qui Nov 28, 2013 18:38
fazendo
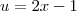
primeiro vamos redefinir os intervalos de integração para a nova variavel
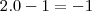
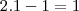
temso que

a integral vai ficar
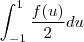
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Qui Nov 28, 2013 22:06
por Pessoa Estranha » Qui Nov 28, 2013 22:06
Olá ! Obrigada pela resposta !
Eu realmente havia escrito como você, mas fiquei na dúvida com relação à função mesmo. O fato de termos uma f(x) que define uma função não implicaria noutra resolução ? Não sei se a minha pergunta é absurda, mas, nos casos mais gerais tínhamos a função com a sua "cara", agora, temos apenas a f aplicada num ponto. Desculpe se estiver falando absurdos ....
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Qui Nov 28, 2013 22:18
por young_jedi » Qui Nov 28, 2013 22:18
Tudo oque ocorreu foi uma mudança de variavel, antes tinhamos uma função de x agora temos um função de u, antes a integral era realizada em x agora sera realizada em u, nao tenho certeza se essa era sua duvida qualquer coisa pode comentar
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Sex Nov 29, 2013 13:34
por Pessoa Estranha » Sex Nov 29, 2013 13:34
Agora melhorou ! Valeu !

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4390 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3541 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Cálculo de integral
por LAZAROTTI » Dom Set 30, 2012 19:52
- 0 Respostas
- 1134 Exibições
- Última mensagem por LAZAROTTI

Dom Set 30, 2012 19:52
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de integral
por jmario » Ter Mai 18, 2010 12:25
- 1 Respostas
- 3188 Exibições
- Última mensagem por MarcosFreitas

Qua Jun 02, 2010 13:04
Cálculo: Limites, Derivadas e Integrais
-
- CALCULO DE INTEGRAL
por Jaison Werner » Sex Jan 07, 2011 18:58
- 4 Respostas
- 3014 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 08, 2011 12:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 contínua em [-1,1]. Calcule
contínua em [-1,1]. Calcule 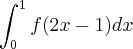 sabendo que
sabendo que 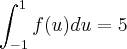 ."
."

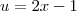
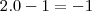
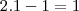

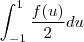

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
