
Teria como resolver sem usar as fórmulas de recorrência ? Tentei resolver sem usa-las, mas cheguei a um resultado totalmente errado !
Obrigada.



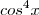 como
como ![[cos^2x]^2 [cos^2x]^2](/latexrender/pictures/1f68a708829330fa456f30b1259b0f32.png) .Para prosseguir , tente reescrever
.Para prosseguir , tente reescrever 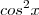 em função de
em função de 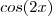 ,logo após , surgirá um termo
,logo após , surgirá um termo 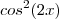 que também pode ser explicitado em termos de
que também pode ser explicitado em termos de 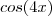 .
.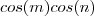 . Somando as expressões abaixo ,
. Somando as expressões abaixo ,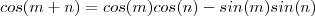
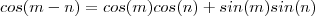
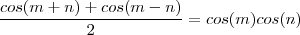 .
.
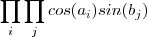 em soma
em soma 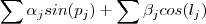



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.