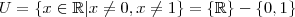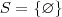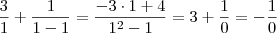por manoelcarlos » Sex Ago 23, 2013 01:21
por manoelcarlos » Sex Ago 23, 2013 01:21
Pessoal, boa noite;
Este é o meu terceiro tópico, cada um com uma dúvida diferente, pois me matriculei em engenharia e preciso relembrar todo o ensino médio: acreditem, estou estudando MUITO pra recuperar esse tempo. Peguei uma equação para tentar resolver, mas não consigo nem dar o primeiro passo desta vez por causa de um x² no denominador. Se alguém puder me ajudar com isso, terá minha eterna gratidão!rs
A equação é
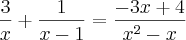
E agora, por onde começar?
-
manoelcarlos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qua Ago 21, 2013 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Luis Gustavo » Sex Ago 23, 2013 13:58
por Luis Gustavo » Sex Ago 23, 2013 13:58
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por manoelcarlos » Seg Ago 26, 2013 01:02
por manoelcarlos » Seg Ago 26, 2013 01:02
Muito obrigado pela resposta, Luis. Como assim "se x for 1, teremos duas divisões por zero"? Não entendi essa parte.
abraço
-
manoelcarlos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qua Ago 21, 2013 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Seg Ago 26, 2013 02:46
por Russman » Seg Ago 26, 2013 02:46
Esta equação é uma equação que degenera para

e

. Veja que se

a primeira parcela, que é

fica

que não faz sentido. Ainda se

a última parcela também degenera, pois
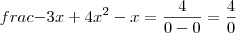
que também não faz sentido assim como pra

pois para este
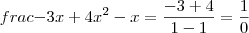
que não faz sentido novamente. Logo, a equação pode admitir valores de

que sejam diferentes de

e

.
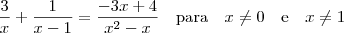
.
Para resolver a equação você deve tentar igualar todos os denominadores. O mínimo múltiplo comum entre eles é uma boa, mas eu prefiro somar as parcelas como fazemos para frações.
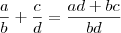
Logo, a equação fica
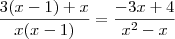

Note que
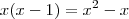
, de modo que os numeradores das frações de cada lado devem ser iguais pois os denominadores já o são. Assim,
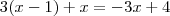
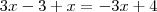
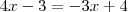
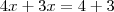


A solução

é da equação
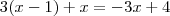
que foi obtida simplificando
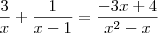
. Mas como para a eq. original excluímos

do conjunto Universo( que são os valores aceitáveis de

) o conjunto Solução da eq. original é vazio. Isto é, não existe valor de

que a satisfaça.
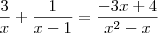
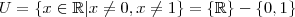
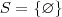
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Luis Gustavo » Seg Ago 26, 2013 15:04
por Luis Gustavo » Seg Ago 26, 2013 15:04
manoelcarlos escreveu:Muito obrigado pela resposta, Luis. Como assim "se x for 1, teremos duas divisões por zero"? Não entendi essa parte.
abraço
É o que o amigo aí em cima disse: Se

, então a equação fica
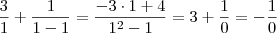
Viu? Temos duas divisões por zero, o que implica que

não é uma solução válida.
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por manoelcarlos » Seg Ago 26, 2013 15:07
por manoelcarlos » Seg Ago 26, 2013 15:07
Russman e Luis Guistavo, muito obrigado pela ajuda. Ainda não absorvi todas as informações, mas vou passar a tarde estudando esse problema. Muito obrigado mesmo!!!!
-
manoelcarlos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qua Ago 21, 2013 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação com Radiciação no denominador
por victorym1 » Ter Mar 24, 2015 21:33
- 0 Respostas
- 1287 Exibições
- Última mensagem por victorym1

Ter Mar 24, 2015 21:33
Equações
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2041 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
-
- [potência] equação
por Ederson_ederson » Qui Jun 25, 2015 08:49
- 1 Respostas
- 1948 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 27, 2015 14:42
Álgebra Elementar
-
- equação com somatório de potência
por dummyman » Sáb Jan 04, 2014 12:28
- 2 Respostas
- 2696 Exibições
- Última mensagem por Russman

Seg Jan 06, 2014 01:24
Álgebra Elementar
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3688 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
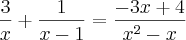


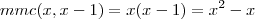
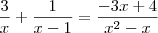
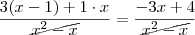
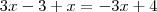


 for
for  , teremos duas divisões por zero D:
, teremos duas divisões por zero D:
 e
e  fica
fica  que não faz sentido. Ainda se
que não faz sentido. Ainda se 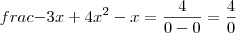 que também não faz sentido assim como pra
que também não faz sentido assim como pra 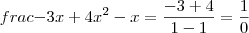 que não faz sentido novamente. Logo, a equação pode admitir valores de
que não faz sentido novamente. Logo, a equação pode admitir valores de  .
.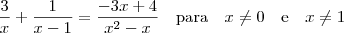 .
.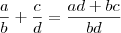
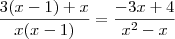

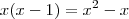 , de modo que os numeradores das frações de cada lado devem ser iguais pois os denominadores já o são. Assim,
, de modo que os numeradores das frações de cada lado devem ser iguais pois os denominadores já o são. Assim,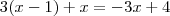
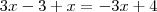
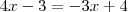
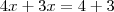

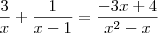 . Mas como para a eq. original excluímos
. Mas como para a eq. original excluímos