 por nakagumahissao » Sáb Jul 13, 2013 09:05
por nakagumahissao » Sáb Jul 13, 2013 09:05
Questão:
![\int_{1}^{\sqrt[2]{3}} \int_{1}^{x} dydx \int_{1}^{\sqrt[2]{3}} \int_{1}^{x} dydx](/latexrender/pictures/9a012373252acfbf99eb31c56e1a324c.png)
O que já fiz: Desenhei em coordenadas cartesianas o gráfico. No gráfico, é fácil de se ver que em 'x', as coordenadas variam de 1 à raiz de três. O mesmo acontece em 'y' pois y = x. Assim, obtive um triângulo retângulo e facilmente pude calcular que a área desejada era de:
![A = 2 - \sqrt[]{3} A = 2 - \sqrt[]{3}](/latexrender/pictures/b20441e32ec4afa5bc59f7eca518ac22.png)
Calculando a integral:
![\int_{1}^{\sqrt[]{3}} \int_{1}^{x} dydx \int_{1}^{\sqrt[]{3}} \int_{1}^{x} dydx](/latexrender/pictures/7e574505b7fed71d13ca5a9fc2437931.png)
pelo modo convencional, também consegui o valor
![A = 2 - \sqrt[]{3} A = 2 - \sqrt[]{3}](/latexrender/pictures/b20441e32ec4afa5bc59f7eca518ac22.png)
. Porém, ao converter para coordenadas polares, não estou conseguindo obter o valor correto obtido pelas formas de cálculo anteriores. Meus parâmetros foram os seguintes:
![\int_{\frac{\pi}{4}}^{\frac{\pi}{6}} \int_{\csc \theta}^{\sqrt[]{3} \csc \theta} dydx \int_{\frac{\pi}{4}}^{\frac{\pi}{6}} \int_{\csc \theta}^{\sqrt[]{3} \csc \theta} dydx](/latexrender/pictures/b7e6afc6a411a064c9d8ff4e3f63ce3a.png)
O que há de errado nos intervalos de integração? Alguém pode ajudar por favor?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por young_jedi » Sáb Jul 13, 2013 11:11
por young_jedi » Sáb Jul 13, 2013 11:11
quando você muda para coordenadas polares a dxdy se torna
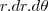
portanto sua integral sera
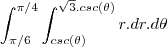
tente resolver e comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por nakagumahissao » Dom Jul 14, 2013 07:52
por nakagumahissao » Dom Jul 14, 2013 07:52
young_jedi,
Obrigado pela resposta. Realmente me esqueci do r. Mas veja bem, se resolvermos a integral, a resposta não vai ser correta. Minha dúvida consiste em saber quais são os intervalos de integração corretos.
Grato
Sandro
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por young_jedi » Dom Jul 14, 2013 11:03
por young_jedi » Dom Jul 14, 2013 11:03
Realmente tem um erro nos limites de integração amigo, obrigado por informar, na verdade o limite superior é secante:
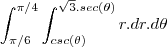
acredito que agora esta certo.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por nakagumahissao » Seg Jul 15, 2013 14:40
por nakagumahissao » Seg Jul 15, 2013 14:40
young_jedi,
Vou tentar resolver desta forma. Obrigado pela ajuda. Enquanto não resolvo, como chegou a conclusão que deveria ser secante ao invés de cossecante?
Grato
Sandro
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por young_jedi » Seg Jul 15, 2013 19:37
por young_jedi » Seg Jul 15, 2013 19:37
tranquilo,
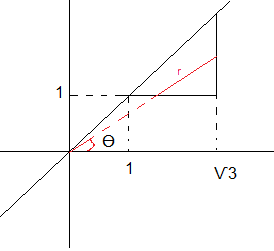
- area.png (2.58 KiB) Exibido 3644 vezes
analisando a figura, temos que a área de integração é o triangulo, se tomarmos um raio r temos que sua variação esta limitada dentro do triangulo pelos dois catetos
sendo que o r vai de
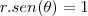
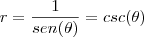
e vai ate
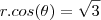
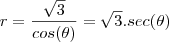
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por nakagumahissao » Ter Jul 16, 2013 09:54
por nakagumahissao » Ter Jul 16, 2013 09:54
young_jedi,
Entendi. Muito obrigado!
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral, coordenadas polares
por manuoliveira » Sáb Nov 24, 2012 19:15
- 2 Respostas
- 2104 Exibições
- Última mensagem por manuoliveira

Dom Nov 25, 2012 21:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Dupla] Em coordenadas polares
por RenatoP » Qui Fev 21, 2013 16:40
- 3 Respostas
- 2294 Exibições
- Última mensagem por young_jedi

Sex Fev 22, 2013 12:25
Cálculo: Limites, Derivadas e Integrais
-
- Integral Dupla em coordenadas polares
por Sobreira » Qua Jun 19, 2013 01:30
- 0 Respostas
- 1531 Exibições
- Última mensagem por Sobreira

Qua Jun 19, 2013 01:30
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de integral dupla por coordenadas polares
por Fernandobertolaccini » Sex Jan 16, 2015 22:13
- 0 Respostas
- 1659 Exibições
- Última mensagem por Fernandobertolaccini

Sex Jan 16, 2015 22:13
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de integral tripla com coordenadas polares
por Fernandobertolaccini » Qua Jan 21, 2015 11:05
- 0 Respostas
- 1359 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jan 21, 2015 11:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{\sqrt[2]{3}} \int_{1}^{x} dydx \int_{1}^{\sqrt[2]{3}} \int_{1}^{x} dydx](/latexrender/pictures/9a012373252acfbf99eb31c56e1a324c.png)
![A = 2 - \sqrt[]{3} A = 2 - \sqrt[]{3}](/latexrender/pictures/b20441e32ec4afa5bc59f7eca518ac22.png)
![\int_{1}^{\sqrt[]{3}} \int_{1}^{x} dydx \int_{1}^{\sqrt[]{3}} \int_{1}^{x} dydx](/latexrender/pictures/7e574505b7fed71d13ca5a9fc2437931.png)
![A = 2 - \sqrt[]{3} A = 2 - \sqrt[]{3}](/latexrender/pictures/b20441e32ec4afa5bc59f7eca518ac22.png) . Porém, ao converter para coordenadas polares, não estou conseguindo obter o valor correto obtido pelas formas de cálculo anteriores. Meus parâmetros foram os seguintes:
. Porém, ao converter para coordenadas polares, não estou conseguindo obter o valor correto obtido pelas formas de cálculo anteriores. Meus parâmetros foram os seguintes:![\int_{\frac{\pi}{4}}^{\frac{\pi}{6}} \int_{\csc \theta}^{\sqrt[]{3} \csc \theta} dydx \int_{\frac{\pi}{4}}^{\frac{\pi}{6}} \int_{\csc \theta}^{\sqrt[]{3} \csc \theta} dydx](/latexrender/pictures/b7e6afc6a411a064c9d8ff4e3f63ce3a.png)


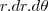
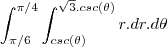
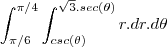
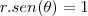
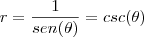
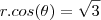
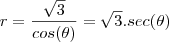
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.