 por chronoss » Seg Abr 22, 2013 20:16
por chronoss » Seg Abr 22, 2013 20:16
3ª Fase: Determine o menor número primo positivo que divide x² + 5x + 23 para algum inteiro x .
Obs: Não estudei congruências ainda, tem como resolver de outros modos?
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Abr 22, 2013 21:22
por e8group » Seg Abr 22, 2013 21:22
Considere
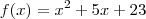
,completando quadrados ,podemos reescrever

como
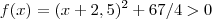
para quaisquer

.Assim ,é fácil ver que
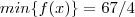
em

.Mas ,como

inteiro ,calculando

e

,obtemos
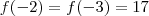
que neste caso , o menor número primo positivo que divide
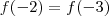
é o próprio 17 .
Tente concluir a parti daí .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Seg Abr 22, 2013 23:22
por chronoss » Seg Abr 22, 2013 23:22
A conclusão não está na ultima linha? Não vejo como acrescentar algo de relevante.
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Ter Abr 23, 2013 11:15
por e8group » Ter Abr 23, 2013 11:15
A conclusão não está na última linha ,mas ela é importante (veremos porque).
Minha estimativa é que 17 seja o menor número primo positivo que divide

,será ?Como provar ?
Sugestões para a solução :
Suponha que exista
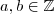
(dependendo de x) tal que
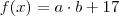
.Se provarmos que de fato existam
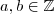
e que o produto deles é par, poderemos concluir que 17 é o menor número primo positivo que divide

(Por quê ?).É isto que vamos fazer .
O número
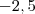
que é ponto de mínimo de

estar compreendido entre
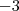
e
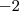
e
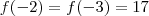
(note que estes valores são raízes da equação
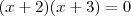
) .Assim ,tomando-se
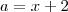
e
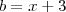
,segue
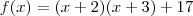
.
O que acontece com o produto

se tomarmos
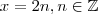
e

,o produto é sempre par (múltiplo de 2)?
Pense sobre isto .
OBS.: Há de ter outra formas de resolver este exercício .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Ter Abr 23, 2013 14:38
por chronoss » Ter Abr 23, 2013 14:38
Obrigado , vou pensar .
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por chronoss » Qui Jul 04, 2013 10:11
por chronoss » Qui Jul 04, 2013 10:11
O raciocínio seria que como ( x + 2 )( x + 3 ) --> sempre par , 17 + par = impar , a função sempre adota valores impares logo ela não é divisível por 2 (primo)??
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Jul 04, 2013 19:00
por e8group » Qui Jul 04, 2013 19:00
Este exercício é interessante .Tenho uma nova idéia .Gostaria de opiniões dos demais usuários .Mas vamos resslatar algumas informações que temos sobre o exercício .Segue elas ...

Sabemos
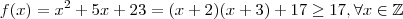
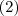
,
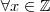
temos sempre

um número par , ou seja ,
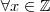
tem-se

um número impar.(Verifique !) .
Quanto a solução , pelo Teorema fundamental da aritmética ,sempre conseguimos números primos
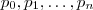
tais que para cada
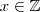
,
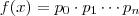
com
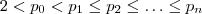
(Observe o item 2) .Assim , definido os números primos ,
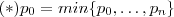
.Agora pelo item (1) ,
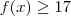
, ou seja ,
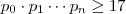
. Logo ,
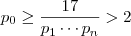
.Vemos então ,
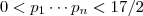
para que
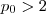
. Mas , o número

é impar e diferente que

,donde obtemos
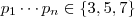
.
Como os números
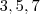
são primos , logo a decomposição

é a trival .Assim ,
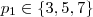
.Se

,isto contraria a hipótese

.Caso fosse
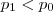
,
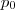
só poderia ser
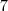
pois
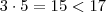
,logo não existe
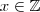
tal que
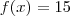
. Caso ,

.Segue ,
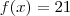
,mas isto implica
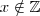
(por favor faça as contas) .Assim , fica evidente que
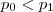
é uma contradição .Para
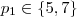
,segue

que não é possível determinar
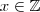
para este caso (Observe as contas acima , basta trocar as letras
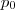
com
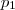
e manter as estruturas algébricas ) .Assim , só podemos ter a decomposição trivial para

.Assim , sendo , segue

logo o menor primo positivo que divide

é

.
Peço desculpas ,não conseguir organizar as idéias da forma que queria devido a falta de tempo .De qualquer forma espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Jul 05, 2013 00:16
por e8group » Sex Jul 05, 2013 00:16
Boa noite .Minha solução está incompleta . Acabei esquecendo de analisar o caso em que

com
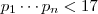
(pois ,se
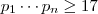
então sempre
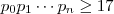
) .Neste caso ,
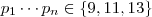
,logo podemos ter
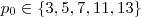
.Além disso,falta analisar o caso em que

.Quando estiver disponível tentarei terminar esta questão .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Jul 05, 2013 12:09
por e8group » Sex Jul 05, 2013 12:09
Bom dia .Mesmo após ter acrescentado aquelas informações pendentes na resolução ,ainda não estou satisfeito com a resolução .Vou continuar pensando sobre esta questão , assim que tiver melhores idéias postarei aqui ,infelizmente só não posso prometer a data pois tenho outras atividades a fazer.Entretanto ,fique à vontade para postar o que entendeu sobre a questão e também sobre como você pensou em desenvolver a mesma. A princípio sem provas , apenas verificando alguns valores inteiros para

,observei a função aplicada a estes valores sempre retornou como resposta um número primo .Se conseguimos provar isto(caso fosse verdade) ,ficaria fácil concluir que o menor primo positivo que divide

é o 17 já que o menor valor que a função assume é 17 que para a nossa sorte é primo .
Aguardo repostas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Dom Jul 07, 2013 14:31
por chronoss » Dom Jul 07, 2013 14:31
Pensei no seguinte para verificar cada caso individualmente :
(1) A função pode ser expressa por : f(x) = ( x + 2 )( x + 3 ) + 17 , que também pode ser representada por : f(n) = 17 + n( n + 1 ) [ com n em função de x ] , que nada mais é que 17 + [ soma dos n primeiros números pares : 2 + 4 + 6 + ... + 2n = n( n + 1 )] ; logo a função sempre adota valores ímpares .
(2) Agora considerando o seguinte teorema :
Se b1 e b2 deixam restos r1 e r2 na divisão por a , respectivamente , então:
b1 + b2 deixa o mesmo resto que r1 + r2 na divisão por a
b1 . b2 deixa o mesmo resto que r1 . r2 na divisão por a.
Analisaremos cada número primo menor que 17 para verificar se dividem a função .
3 | f(x) => 3 | f(n) => 3 | 17 + n( n + 1 ) ; seja : 17 = b1 , n( n + 1 ) = b2 onde concluímos pelo teorema que : 3 | f(n) se e somente se : a soma dos restos r1 e r2 , de b1 e b2 (respectivamente) , deixar resto 0 quando dividida por 3 , ou seja se : 3 | ( r1 + r2 ).
Os possíveis restos na divisão por 3 são : 0 , 1 , 2 .
17 deixa resto igual a 2 , quando dividido por 3 , logo r2 deve ser igual a 1 para que afirmação : 3 | f(n) seja verdadeira .
r2 = 1 , se e somente se : o produto dos restos r3 e r4 das de divisões de n e ( n + 1 ) por 3 for igual a 1 .
Fazendo uma verificação baseada no teorema apresentado :
n (n) + n(1) = 1 <--> r3 ( r3) + r3 ( 1 ) = 1 <--> (r3)² + r3 = 1 <--> (r3)² + r3 - 1 = 0 ; cujas raízes são : 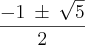 .
.
Que não é um resultado válido , pois sabemos que se n e 3 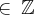 , então o resto r3 , da divisão de n por 3 ,
, então o resto r3 , da divisão de n por 3 , 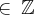 .
.
Provando que a afirmação : 3 | f(n) é falsa  a afirmação 3 | f(x) também é falsa .
a afirmação 3 | f(x) também é falsa .
Após verificar de forma análoga os outros números primos menores que 17 : { 5 , 7 , 11 , 13 } , concluímos que 17 é o menor número primo que divide f(x) , para algum inteiro x .
Obs: No raciocínio usado foram considerados apenas os valores de x inteiros  , pois o gráfico da função é uma parábola .
, pois o gráfico da função é uma parábola .
Ps : Santhiago , gostaria de sua ajuda e dos demais usuários para verificar se o raciocínio contém erros , inconsistência ou escassez de informação . E por favor não riam se cometi algum erro ridiculamente tosco . 


-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Jul 07, 2013 17:42
por e8group » Dom Jul 07, 2013 17:42
Na minha opinião sua solução está globalmente correta,vamos ver o que os demais usuários do fórum acham.Se permite-me ,gostaria de palpitar novamente,desta vez vou incluir seu raciocínio na minha resolução .
Consideremos
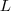
o subconjunto do conjunto dos números primos impares.Suponhamos que para cada
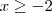
ou
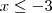
inteiro (pois a função

não é injetiva ,para cada
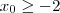
inteiro existe algum
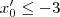
inteiro tal que

) conseguimos números (dependendo de

) primos
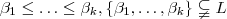
tal que o número composto

pode ser reescrito como
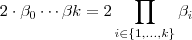
.Assim , sendo
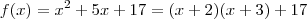
. Segue ,
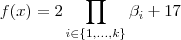
.Além disso ,para cada
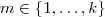
, temos
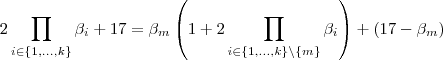
.Ou seja ,
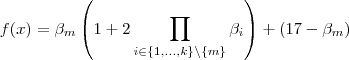
.
Vemos então que se
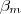
divide

tem-se necessariamente

(Por quê ? ) .Agora suponhamos
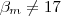
.Pela infinitude dos números primos conseguimos números primos impares distintos dos
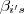
tais que eles dividem f(x).Assim se
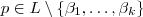
podemos supor que
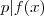
e utilizar o item proposto por você (2) " ...Agora considerando o seguinte teorema : ..." em diante para concluir que

necessariamente é estritamente maior que 17 .
Editado pela última vez por
e8group em Seg Jul 08, 2013 17:57, em um total de 1 vez.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Jul 07, 2013 18:02
por e8group » Dom Jul 07, 2013 18:02
OBS.: Na verdade ,o produto
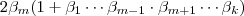
seria
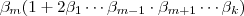
o correto que de forma compacta é :
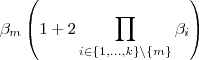
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Seg Jul 08, 2013 17:24
por chronoss » Seg Jul 08, 2013 17:24
Ainda estou tentando entender seu raciocínio , deste ponto : Além disso ,para cada m ... , em diante ficou meio confuso para mim.
Obs: No começo vc citou que a função é injetiva , mas a definição de função injetiva não seria justamente o contrário? E também para o produtório ser de números primos , x deveria ser maior que ( - 1 ) ou menor que ( - 4 ) , ou não??
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Jul 08, 2013 17:53
por e8group » Seg Jul 08, 2013 17:53
Tem razão . Na verdade queria dizer que ela não era injetora (assim basta analisar um subconjunto de seu dominío onde a função é injetiva ).Estar editado .Obrigado .
Note que ,
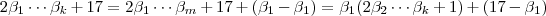
.
De forma análoga ,

(...)

.
Assim , podemos dizer que para escolha arbitrária de

em

temos :

ou de forma compacta conforme eu já postei .Utilizei esta introdução apenas para mostra que se alguns dos números primos da lista divide

então necessariamente ele é
. Aparti daí usei o fato da infinidade dos números primos para obtermos números primos que não está na lista (já postada) que divide

e então mostrar que tais números são necessariamente maiores que 17 (usando seu raciocínio) .
Em resumo , no fundo não fiz nada demais . Minha solução proposta difere da sua apenas na introdução ,o restante da questão é globalmente análoga a sua no meu ponto de vista .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Jul 08, 2013 19:27
por e8group » Seg Jul 08, 2013 19:27
Correto .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Seg Jul 08, 2013 19:57
por chronoss » Seg Jul 08, 2013 19:57
Obrigado por toda a ajuda santhiago , toda a discussão foi bastante agradável .
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Jul 08, 2013 21:26
por e8group » Seg Jul 08, 2013 21:26
Não há de quê .Se tiver mais questões aí para compartilhar, a comunidade a agradece .De qualquer forma,se você disse que esta questão foi resolvida usando relações de congruências, talvez seja melhor assim .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- CN 2003
por Georges123 » Sáb Mai 18, 2013 16:39
- 1 Respostas
- 1517 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 17:46
Teoria dos Números
-
- Problema (Enem 2003)
por Karina » Sáb Mar 27, 2010 13:57
- 2 Respostas
- 4214 Exibições
- Última mensagem por Karina

Sáb Mar 27, 2010 19:26
Álgebra Elementar
-
- MAE1511 - trabalho em grupo - 2003
 por admin » Ter Abr 22, 2008 21:14
por admin » Ter Abr 22, 2008 21:14
- 0 Respostas
- 1582 Exibições
- Última mensagem por admin

Ter Abr 22, 2008 21:14
Estatística para Licenciatura I
-
- MAE1511 - trabalho em grupo 4 - 2003
 por admin » Ter Abr 22, 2008 21:26
por admin » Ter Abr 22, 2008 21:26
- 0 Respostas
- 1521 Exibições
- Última mensagem por admin

Ter Abr 22, 2008 21:26
Estatística para Licenciatura I
-
- MAE1511 - trabalho em grupo 3 - 2003
 por admin » Ter Abr 22, 2008 21:39
por admin » Ter Abr 22, 2008 21:39
- 0 Respostas
- 1530 Exibições
- Última mensagem por admin

Ter Abr 22, 2008 21:39
Estatística para Licenciatura I
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



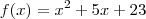 ,completando quadrados ,podemos reescrever
,completando quadrados ,podemos reescrever  como
como 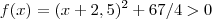 para quaisquer
para quaisquer  .Assim ,é fácil ver que
.Assim ,é fácil ver que 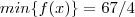 em
em  .Mas ,como
.Mas ,como  inteiro ,calculando
inteiro ,calculando  e
e  ,obtemos
,obtemos 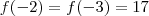 que neste caso , o menor número primo positivo que divide
que neste caso , o menor número primo positivo que divide 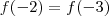 é o próprio 17 .
é o próprio 17 .

 ,será ?Como provar ?
,será ?Como provar ?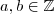 (dependendo de x) tal que
(dependendo de x) tal que 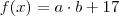 .Se provarmos que de fato existam
.Se provarmos que de fato existam 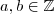 e que o produto deles é par, poderemos concluir que 17 é o menor número primo positivo que divide
e que o produto deles é par, poderemos concluir que 17 é o menor número primo positivo que divide  (Por quê ?).É isto que vamos fazer .
(Por quê ?).É isto que vamos fazer .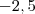 que é ponto de mínimo de
que é ponto de mínimo de  estar compreendido entre
estar compreendido entre 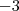 e
e 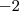 e
e 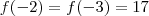 (note que estes valores são raízes da equação
(note que estes valores são raízes da equação 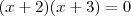 ) .Assim ,tomando-se
) .Assim ,tomando-se 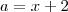 e
e 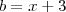 ,segue
,segue 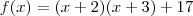 .
. se tomarmos
se tomarmos 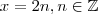 e
e  ,o produto é sempre par (múltiplo de 2)?
,o produto é sempre par (múltiplo de 2)? 


 Sabemos
Sabemos 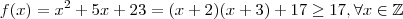
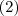 ,
, 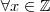 temos sempre
temos sempre  um número par , ou seja ,
um número par , ou seja , 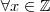 tem-se
tem-se  um número impar.(Verifique !) .
um número impar.(Verifique !) .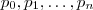 tais que para cada
tais que para cada 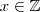 ,
, 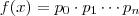 com
com 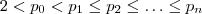 (Observe o item 2) .Assim , definido os números primos ,
(Observe o item 2) .Assim , definido os números primos , 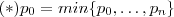 .Agora pelo item (1) ,
.Agora pelo item (1) , 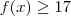 , ou seja ,
, ou seja , 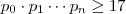 . Logo ,
. Logo , 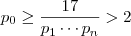 .Vemos então ,
.Vemos então , 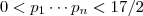 para que
para que 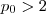 . Mas , o número
. Mas , o número  é impar e diferente que
é impar e diferente que  ,donde obtemos
,donde obtemos 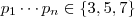 .
. 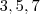 são primos , logo a decomposição
são primos , logo a decomposição  é a trival .Assim ,
é a trival .Assim , 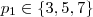 .Se
.Se  ,isto contraria a hipótese
,isto contraria a hipótese  .Caso fosse
.Caso fosse 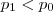 ,
,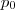 só poderia ser
só poderia ser 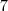 pois
pois 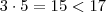 ,logo não existe
,logo não existe 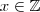 tal que
tal que 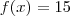 . Caso ,
. Caso , .Segue ,
.Segue , 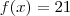 ,mas isto implica
,mas isto implica 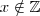 (por favor faça as contas) .Assim , fica evidente que
(por favor faça as contas) .Assim , fica evidente que 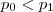 é uma contradição .Para
é uma contradição .Para 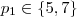 ,segue
,segue  que não é possível determinar
que não é possível determinar 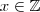 para este caso (Observe as contas acima , basta trocar as letras
para este caso (Observe as contas acima , basta trocar as letras 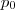 com
com 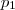 e manter as estruturas algébricas ) .Assim , só podemos ter a decomposição trivial para
e manter as estruturas algébricas ) .Assim , só podemos ter a decomposição trivial para  .Assim , sendo , segue
.Assim , sendo , segue  logo o menor primo positivo que divide
logo o menor primo positivo que divide  é
é  .
.
 com
com 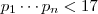 (pois ,se
(pois ,se 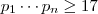 então sempre
então sempre 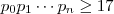 ) .Neste caso ,
) .Neste caso , 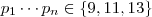 ,logo podemos ter
,logo podemos ter 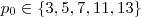 .Além disso,falta analisar o caso em que
.Além disso,falta analisar o caso em que  .Quando estiver disponível tentarei terminar esta questão .
.Quando estiver disponível tentarei terminar esta questão .


 ,observei a função aplicada a estes valores sempre retornou como resposta um número primo .Se conseguimos provar isto(caso fosse verdade) ,ficaria fácil concluir que o menor primo positivo que divide
,observei a função aplicada a estes valores sempre retornou como resposta um número primo .Se conseguimos provar isto(caso fosse verdade) ,ficaria fácil concluir que o menor primo positivo que divide  é o 17 já que o menor valor que a função assume é 17 que para a nossa sorte é primo .
é o 17 já que o menor valor que a função assume é 17 que para a nossa sorte é primo . 

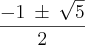 .
.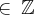 , então o resto r3 , da divisão de n por 3 ,
, então o resto r3 , da divisão de n por 3 , 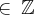 .
.  a afirmação 3 | f(x) também é falsa .
a afirmação 3 | f(x) também é falsa . , pois o gráfico da função é uma parábola .
, pois o gráfico da função é uma parábola .
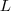 o subconjunto do conjunto dos números primos impares.Suponhamos que para cada
o subconjunto do conjunto dos números primos impares.Suponhamos que para cada 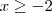 ou
ou 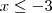 inteiro (pois a função
inteiro (pois a função  não é injetiva ,para cada
não é injetiva ,para cada 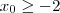 inteiro existe algum
inteiro existe algum 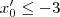 inteiro tal que
inteiro tal que  ) conseguimos números (dependendo de
) conseguimos números (dependendo de  ) primos
) primos 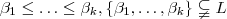 tal que o número composto
tal que o número composto  pode ser reescrito como
pode ser reescrito como 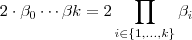 .Assim , sendo
.Assim , sendo 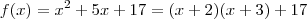 . Segue ,
. Segue , 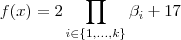 .Além disso ,para cada
.Além disso ,para cada 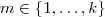 , temos
, temos 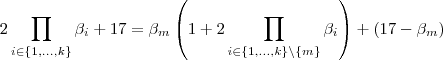 .Ou seja ,
.Ou seja , 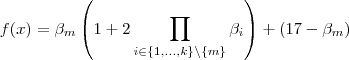 .
. 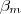 divide
divide  tem-se necessariamente
tem-se necessariamente  (Por quê ? ) .Agora suponhamos
(Por quê ? ) .Agora suponhamos 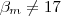 .Pela infinitude dos números primos conseguimos números primos impares distintos dos
.Pela infinitude dos números primos conseguimos números primos impares distintos dos 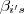 tais que eles dividem f(x).Assim se
tais que eles dividem f(x).Assim se 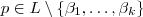 podemos supor que
podemos supor que 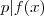 e utilizar o item proposto por você (2) " ...Agora considerando o seguinte teorema : ..." em diante para concluir que
e utilizar o item proposto por você (2) " ...Agora considerando o seguinte teorema : ..." em diante para concluir que  necessariamente é estritamente maior que 17 .
necessariamente é estritamente maior que 17 .
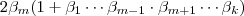 seria
seria 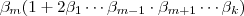 o correto que de forma compacta é :
o correto que de forma compacta é : 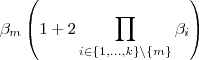 .
.

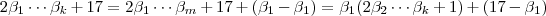 .
. 
 .
.  em
em  temos :
temos : 
 então necessariamente ele é
então necessariamente ele é 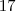 . Aparti daí usei o fato da infinidade dos números primos para obtermos números primos que não está na lista (já postada) que divide
. Aparti daí usei o fato da infinidade dos números primos para obtermos números primos que não está na lista (já postada) que divide  e então mostrar que tais números são necessariamente maiores que 17 (usando seu raciocínio) .
e então mostrar que tais números são necessariamente maiores que 17 (usando seu raciocínio) . 
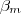 adotar valor = 17 , o valor de x considerado não é ( -2 ) ou (-3) , pois se fosse , o produtório perderia o sentido depois da função ser dividida por
adotar valor = 17 , o valor de x considerado não é ( -2 ) ou (-3) , pois se fosse , o produtório perderia o sentido depois da função ser dividida por 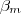 . Certo?
. Certo?





 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
